题目列表(包括答案和解析)
函数y＝1－2
的最小值、最大值分别是（ ）
A．－1，3 B．－1，1 C．0，3 D．0，1
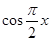的最小值、最大值分别是（ ）| A．－1，3 | B．－1，1 | C．0，3 | D．0，1 |
设函数y＝f(x)是奇函数，对于任意x、y∈R都有f(x＋y)＝f(x)＋f(y)，且当x＞0时，y＜0，f(1)＝－2．求函数y＝f(x)在区间[－3，3]上的最大值和最小值．
最小正周期为π的函数
(其中a是小于零的常数，
是大于零的常数)的图象按向量
，(0＜θ＜π)平移后得到函数y＝f(x)的图象，而函数y＝f(x)在实数集上的值域为[－2，2]，且在区间
上是单调递减函数．
(1)求a、
和θ的值；
(2)若角α和β的终边不共线，f(α)＋g(α)＝f(β)＋g(β)，求tan(α＋β)的值．
设函数f(x)的定义域为R，对于任意的实数x、y都有f(x＋y)＝f(x)＋f(y)，又当x＞0时，f(x)＜0，且f(2)＝－1．
(1)求证：f(x)为奇函数；
(2)试问函数f(x)在区间[－6，6]上是否存在最大值与最小值？若存在，求出最大值、最小值；若不存在，请说明理由．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com