（本题满分12分） 已知盒子中有4个红球，n个白球，若从中一次取出4个球，其中白球的个数为X，且

   （I）求n的值；

   （II）若从中不放回地逐一抽取，取到所有白球则停止抽取。在前3次取球中恰取到1个白球的条件下，共需取球Y次，求Y的分布列和E（Y）。

（本题满分10分）在一个口袋中装有12个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球，得到红球的概率是，从袋中任意摸出2个球，至少得到一个黑球的概率是。

求：（1）袋中黑球的个数；

（2）从袋中任意摸出3个球，至少得到2个黑球的概率。（结果用分数表示）

（本题满分12分）盒中有5个红球，11个蓝球。红球中有2个玻璃球，3个木质球；蓝球中有4个玻璃球，7个木质球。现从中任取一球，假设每个球摸到的可能性都相同，若已知取到的球是玻璃球，求它是蓝球的概率。

(本题分12分）

从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同．

（Ⅰ）若抽取后又放回,抽取3次,求恰好抽到2次为红球的概率;

（Ⅱ）若抽取后不放回,设抽完红球所需的次数为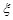,求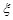的分布列及期望．

      〈本题满分12分〉甲、乙两同学进行投篮比赛，每一简每人各投两次球，规定进球数多者该局获胜，进球数相同则为平局.已知甲每次投进的概率为2/3乙每次投进的概率为1/2，甲、乙之间的投篮相互独立.

(1) 求甲、乙两同学进行一扃比赛的结果不是平局的概率；

(2) 设3局比赛中，甲每局进两球获胜的局数为。求的分布列及数学期望.