
题目列表(包括答案和解析)
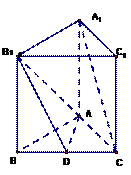
(本题12分)如图,在直三棱柱(侧棱与底面垂直的三棱柱)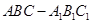 中,
中,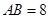 ,
,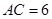 ,
,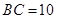 ,
,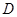 是
是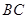 边的中点.
边的中点.
(Ⅰ)求证: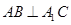 ;
;
(Ⅱ)求证: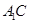 ∥ 面
∥ 面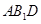 .
.

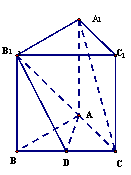 (本题12分)如图,在直三棱柱(侧棱与底面垂直的三棱柱)
(本题12分)如图,在直三棱柱(侧棱与底面垂直的三棱柱)![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 边的中点.
边的中点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() ∥ 面
∥ 面![]() .
.
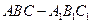 中,
中,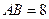 ,
,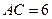 ,
,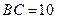 ,
,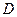 是
是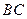 边的中点.
边的中点.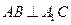 ;
; 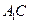 ∥面
∥面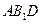 .
. 
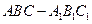 的底面是直角三角形,
的底面是直角三角形,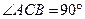 ,点
,点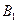 在底面
在底面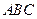 上的射影恰好是
上的射影恰好是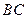 的中点,且
的中点,且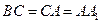 .
.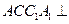 平面
平面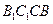 ;
;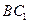
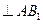 ;
;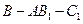 的大小.
的大小. 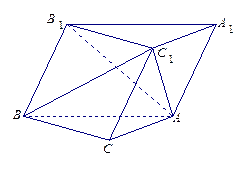
已知直三棱柱 中,
中,  ,
, ,
,
 是
是 和
和 的交点, 若
的交点, 若 .
.
(1)求 的长; (2)求点
的长; (2)求点 到平面
到平面 的距离;
的距离;
(3)求二面角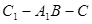 的平面角的正弦值的大小.
的平面角的正弦值的大小.

【解析】本试题主要考查了距离和角的求解运用。第一问中,利用ACC A
A 为正方形,
为正方形,  AC=3
AC=3
第二问中,利用面BB C
C C内作CD
C内作CD BC
BC ,
则CD就是点C平面A
,
则CD就是点C平面A BC
BC 的距离CD=
的距离CD= ,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
解法一: (1)连AC 交A
交A C于E, 易证ACC
C于E, 易证ACC A
A 为正方形,
为正方形,  AC=3
…………… 5分
AC=3
…………… 5分
(2)在面BB C
C C内作CD
C内作CD BC
BC ,
则CD就是点C平面A
,
则CD就是点C平面A BC
BC 的距离CD=
的距离CD= … 8分
… 8分
(3) 易得AC
 面A
面A CB,
过E作EH
CB,
过E作EH A
A B于H, 连HC
B于H, 连HC ,
则HC
,
则HC
 A
A B
B

 C
C HE为二面角C
HE为二面角C -A
-A B-C的平面角. ……… 9分
B-C的平面角. ……… 9分
 sin
sin C
C HE=
HE=
 二面角C
二面角C -A
-A B-C的平面角的正弦大小为
B-C的平面角的正弦大小为 ……… 12分
……… 12分
解法二: (1)分别以直线C B、CC
B、CC 、C
、C A为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C
A为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C (0,
0, 0), B
(0,
0, 0), B (4,
0, 0), B(4, -3, 0), C(0, -3,
0), A
(4,
0, 0), B(4, -3, 0), C(0, -3,
0), A (0,
0, h), A(0, -3, h), G(2, -
(0,
0, h), A(0, -3, h), G(2, - , -
, - ) ……………………… 3分
) ……………………… 3分

 =(2, -
=(2, - , -
, - ),
),  =(0,
-3, -h) ……… 4分
=(0,
-3, -h) ……… 4分

 ·
· =0,
=0,
 h=3
h=3
(2)设平面A BC
BC 得法向量
得法向量 =(a, b, c),则可求得
=(a, b, c),则可求得 =(3, 4, 0) (令a=3)
=(3, 4, 0) (令a=3)
 点A到平面A
点A到平面A BC
BC 的距离为H=|
的距离为H=| |=
|= ……… 8分
……… 8分
(3) 设平面A BC的法向量为
BC的法向量为 =(x, y, z),则可求得
=(x, y, z),则可求得 =(0, 1, 1) (令z=1)
=(0, 1, 1) (令z=1)
 二面角C
二面角C -A
-A B-C的大小
B-C的大小 满足cos
满足cos =
= =
= ………
11分
………
11分
 二面角C
二面角C -A
-A B-C的平面角的正弦大小为
B-C的平面角的正弦大小为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com