（本题满分14分）一个袋中装有大小和质地都相同的10个球，其中黑球4个，白球5个，红球1个。

（1）从袋中任意摸出3个球，记得到白球的个数为X，求随机变量X的概率分布和数学期望E(X);

（2）每次从袋中随机地摸出一球，记下颜色后放回.求3次摸球后，摸到黑球的次数大于摸到白球的次数的概率。

（本小题满分12分）

一个不透明的袋子中装有4个形状相同的小球，分别标有不同的数字2，3，4，，现从袋中随机摸出2个球，并计算摸出的这2个球上的数字之和，记录后将小球放回袋中搅匀，进行重复试验。记A事件为“数字之和为7”.试验数据如下表

（参考数据：）

（Ⅰ）如果试验继续下去，根据上表数据，出现“数字之和为7”的频率将稳定在它的概率附近。试估计“出现数字之和为7”的概率，并求的值；

（Ⅱ）在（Ⅰ）的条件下，设定一种游戏规则：每次摸2球，若数字和为7，则可获得奖金7元，否则需交5元。某人摸球3次，设其获利金额为随机变量元，求的数学期望和方差。

(本小题满分14分)

一只袋中装有2个白球、3个红球，这些球除颜色外都相同。

  （Ⅰ）从袋中任意摸出1个球，求摸到的球是白球的概率；

  （Ⅱ）从袋中任意摸出2个球，求摸出的两个球都是白球的概率；

  （Ⅲ）从袋中任意摸出2个球，求摸出的两个球颜色不同的概率。

（本题满分14分）

已知箱中装有4个白球和5个黑球，且规定：取出一个白球的2分，取出一个黑球的1分．

现从该箱中任取 ( 无放回 ) 3个球，记随机变量X为取出3球所得分数之和．

(Ⅰ) 求X的分布列；

(Ⅱ) 求X的数学期望E(X)．

（本小题满分14分）

袋中装有黑球和白球共7个，从中任取1个球是白球的概率为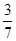．现有甲、乙两人从袋中轮流摸取1球，取后不放回：甲先取，乙后取，然后甲再取……，直到两人中有一人取到白球时即终止．每个球在每一次被取出的机会是等可能的．

（1）求取球2次终止的概率；

（2）求甲取到白球的概率．