
题目列表(包括答案和解析)
某港口的水深 (米)是时间
(米)是时间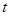 (
( ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
|
10 |
13 |
9.9 |
7 |
10 |
13 |
10.1 |
7 |
10 |
经过长期观测,  可近似的看成是函数
可近似的看成是函数 ,(本小题满分14分)
,(本小题满分14分)
(1)根据以上数据,求出 的解析式。
的解析式。
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
【解析】第一问由表中数据可以看到:水深最大值为13,最小值为7,,
∴A+b=13, -A+b=7 解得 A=3, b=10
第二问要想船舶安全,必须深度 ,即
,即
∴

解得:
 得到结论。
得到结论。
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当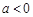 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
箱子里有3双不同的手套,随机地拿出2只,记事件A={拿出的手套配不成对};事件B={拿出的都是同一只手上的手套};事件C={拿出的手套一只是左手的,一只是右手的,但配不成对}。(本小题满分13分)
(1)请罗列出所有的基本事件;
(2)分别求事件A、事件B、事件C的概率;
(3)说出事件A、事件B、事件C的关系。
【解析】第一问利用分别设3双手套为:
 ;
;
 ;
;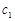
 。
。  、
、 、
、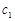 分别代表左手手套,
分别代表左手手套, 、
、 、
、 分别代表右手手套。
分别代表右手手套。
第二问①事件A包含12个基本事件,故P(A)= 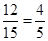 ,(或能配对的只有3个基本事件,
,(或能配对的只有3个基本事件,
P(A)= 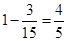 );
);
②事件B包含6个基本事件,故P(B)= 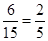 ;
;
事件C包含6个基本事件,故P(C)= 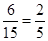
第三问
解:(1)分别设3双手套为:
 ;
;
 ;
;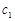
 。
。  、
、 、
、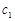 分别代表左手手套,
分别代表左手手套, 、
、 、
、 分别代表右手手套。…………2分
分别代表右手手套。…………2分
箱子里 的3双不同的手套,随机地拿出2只,所有的基本事件是:
( ,
, )、(
)、( ,
,
 )、(
)、( ,
, )、(
)、( ,
,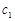 )、(
)、( ,
, )
)
( ,
, )、(
)、( ,
, )、(
)、( ,
,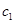 )、(
)、( ,
, );
);
( ,
, )、(
)、( ,
,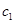 )、(
)、( ,
, )
)
( ,
,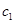 )、(
)、( ,
, )、(
)、(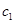 ,
, ) 共15个基本事件。 ……………5分
) 共15个基本事件。 ……………5分
(2)①事件A包含12个基本事件,故P(A)= 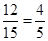 ,(或能配对的只有3个基本事件,
,(或能配对的只有3个基本事件,
P(A)= 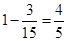 );
……………7分
);
……………7分
②事件B包含6个基本事件,故P(B)= 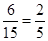 ;…………9分
;…………9分
③事件C包含6个基本事件,故P(C)= 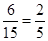 。…………11分
。…………11分
⑶ 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com