
题目列表(包括答案和解析)
| 动作 | K动作 | D动作 | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 |  |  |  |  |
| 动作 | K动作 | D动作 | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 |  |  |  |  |
 的分布列及数学期望
的分布列及数学期望
(本小题满分12分)
2010年广东亚运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K
和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员
的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前
训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
|
动作 |
K |
D |
||
|
得分 |
100 |
80 |
40 |
10 |
|
概率 |
|
|
|
|
乙系列:
|
动作 |
K |
D |
||
|
得分 |
90 |
50 |
20 |
0 |
|
概率 |
|
|
|
|
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(1)若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(2)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX.
(本小题满分12分)2010年广东亚运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
|
动作 |
K |
D |
||
|
得分 |
100 |
80 |
40 |
10 |
|
概率 |
|
|
|
|
乙系列:
|
动作 |
K |
D |
||
|
得分 |
90 |
50 |
20 |
0 |
|
概率 |
|
|
|
|
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(I) 若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(II) (II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX。
(本小题满分12分)
2011年深圳大运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D
两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。假
设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某
运动员完成甲系列和乙系列的情况如下表:
甲系列:
|
动作 |
K |
D |
||
|
得分 |
100 |
80 |
40 |
10 |
|
概率 |
|
|
|
|
乙系列:
|
动作 |
K |
D |
||
|
得分 |
90 |
50 |
20 |
0 |
|
概率 |
|
|
|
|
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(I)若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一
名的概率;
(II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX。
(本小题满分12分)
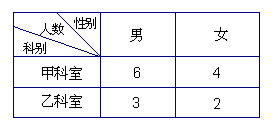
某单位甲乙两个科室人数及男女工作人员分布情况见右表.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两个科室中共抽取3名工作人员进行一项关于“低碳生活”的调查.
(1)求从甲、乙两科室各抽取的人数;
(2)求从甲科室抽取的工作人员中至少有1名女性的概率;
(3)记![]() 表示抽取的3名工作人员中男性的人数,求
表示抽取的3名工作人员中男性的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com