
题目列表(包括答案和解析)
(本小题满分12分)
第8届中学生模拟联合国大会将在本校举行,为了搞好接待工作,组委会招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如下茎叶图(单位:cm):

 男 女
男 女
 15
7 7 8 9 9 9
15
7 7 8 9 9 9
9 8 16 0 0 1 2 4 5 8 9
8 6 5 0 17 2 5 6
7 4 2 1 18 0
1 0 19
若男生身高在180cm以上(包括180cm)定义为“高个子”, 在180cm以下(不包括180cm)定义为“非高个子”, 女生身高在170cm以上(包括170cm)定义为“高个子”,在170cm以下(不包括170cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人,则应分别抽取“高个子”、“非高个子”各几人?
(2)从(1)中抽出的6人中选2人担任领座员,那么至少有一人是“高个子”的概率是多少?
三.解答题(解答应写出文字说明,证明过程或演算步骤):
17. (本小题满分12分)
已知等比数列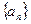 中,
中,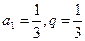 ,
,
(1)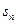 为数列
为数列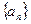 前
前 项的和,证明:
项的和,证明:
(2)设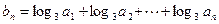 ,求数列
,求数列 的通项公式;
的通项公式;
(本小题满分12分)
某班t名学生在2011年某次数学测试中,成绩全部介于80分与130分之间,将测试结果按如下方式分成五组,第一组[80,90);第二组[90,100)…第五组
[120,130],下表是按上述分组方法得到的频率分布表:
|
分组 |
频数 |
频率 |
|
[80,90) |
x |
0.04 |
|
[90,100) |
9 |
y |
|
[100,110) |
z |
0.38 |
|
[110,120) |
17 |
0.34 |
|
[120,130] |
3 |
0.06 |
(Ⅰ) 求t及分布表中x,y,z的值;
(Ⅱ)设m,n是从第一组或第五组中任意抽取的两名学生的数学测试成绩,求事件
“|m—n|≤10”的概率.
(本小题满分12分)
已知斜率为1的直线1与双曲线C:![]() 相交于B、D两点,且BD的中点为M(1.3)
相交于B、D两点,且BD的中点为M(1.3)
(Ⅰ)(Ⅰ)求C的离心率;
(Ⅱ)(Ⅱ)设C的右顶点为A,右焦点为F,|DF|·|BF|=17证明:过A、B、D三点的圆与x轴相切。
(本小题满分12分)
某班全部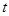 名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是按上述分组方式得到的频率分布表。
名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是按上述分组方式得到的频率分布表。
|
分 组 |
频数 |
频率 |
|
[13,14) |
|
|
|
[14,15) |
|
|
|
[15,16) |
|
|
|
[16,17) |
|
|
|
[17,18] |
|
|
(1)求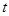 及上表中的
及上表中的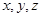 的值;
的值;
(2)设m,n是从第一组或第五组中任意抽取的两名学生的百米测试成绩,求事件“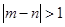 ”的概率.
”的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com