4、真空中存在空间范围足够大的、水平向右的匀强电场。在电场中，若将一个质量为m带正电的小球由静止释放，运动中小球的速度与竖直方向夹角为53º(取sin37º=0.6，cos37º=0.8)。现将该小球从电场中某点以v₀=10m/s的初速度竖直向上抛出。求运动过程中

(1)小球受到的电场力的大小和方向；

(2)小球从抛出点至最高点的电势能变化量；

(3)小球的最小动量的大小和方向。

3、如图所示，原来静止在水平面上的长纸带上放有一个质量为m的小金属块A。金属块离纸带左端距离为d，与纸带间动摩擦因数为μ。现用力向右将纸带从金属块下面抽出，设纸带的加速过程极短，可以认为一开始抽动纸带就做匀速运动。求：⑴金属块刚开始运动时所受的摩擦力大小和方向。⑵为了能把纸带从金属块下面抽出，纸带的速度v应满足什么条件？

2、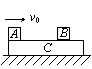如图所示，在光滑水平面上放有一个长为L的长木板C，在C左端和距左端s处各放有一个小物块A、B，A、B都可视为质点，它们与C之间的动摩擦因数都是μ，A、B、C的质量都是m。开始时B、C静止，A以某一初速度v₀向右运动。设B与C之间的最大静摩擦力等于滑动摩擦力。求：⑴A相对于C向右滑动过程中，B与C之间的摩擦力大小。⑵为使A、B能够相碰，A的初速度v₀应满足什么条件？

1、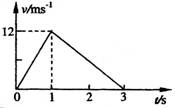如图所示，质量为1kg的物体静置在水平地面上，现对物体施以水平方向的恒定拉力，1s末将拉力撤去，物体运动的v-t图象如图所示，试求：

(1)在0-3s内物体的位移；

(2)滑动摩擦力的大小；

(3)拉力的大小。

30.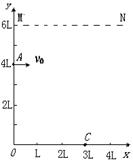(2006年梧州市高三一模)(20分)如图所示，在xoy平面内，MN和x轴之间有平行于y轴的匀强电场和垂直于xoy平面的匀强磁场，y轴上离坐标原点4L的A点处有一电子枪，可以沿+x方向射出速度为v₀的电子(质量为m，电量为e). 如果电场和磁场同时存在，电子将做匀速直线运动.如果撤去电场，只保留磁场，电子将从x轴上距坐标原点3L的C点离开磁场.不计重力的影响，求：(1)磁感应强度B和电场强度E的大小和方向；(2)如果撤去磁场，只保留电场，电子将从D点(图中未标出)离开电场，求D点的X轴坐标？

计算论述题专项训练(十)答案

10-1．设：推进器产生的恒力为F，未放被测物块时小车加速度为a₁，则根据牛顿第二定律及运动规律可得：F=ma₁……(1)　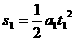　 ……(2)

放上被测物块后，系统加速度为a₂，则有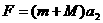：……(3)

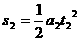……(4)　　　 代入数值后可解得：M=1.25kg

10-2．

10-3解：(1)只有磁场时，电子运动轨迹如图1所示

洛仑兹力提供向心力 (2分)　　 由几何关系 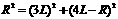　　　　　得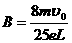：　 　　　(2分)　　　　　 方向： 垂直纸面向里　　 　　 (2分)

　电子做匀速直线运动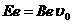 (2分)　 　求得　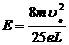　　　　　　 (2分)

方向沿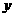轴负方向　 　 (2分)

(2)只有电场时，电子从MN上的D点离开电场，如图2所示

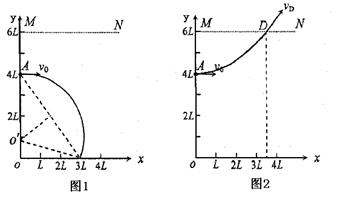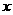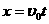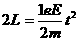设D点横坐标为，(2分)　 　(2分)

求出D点的X坐标为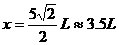 (2分)

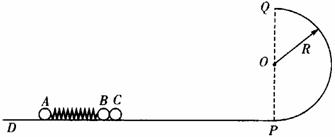
29.(武汉2006年3月)如图所示，光滑轨道的DP段为水平直轨道，PQ段为半径是R的竖直半圆轨道，半圆轨道的下端与水平轨道的右端相切于P点。一轻质弹簧两端分别固定质量为2m的小球A和质量为m的小球B，质量为m的小球C靠在B球的右侧。现用外力作用在A和C上，弹簧被压缩(弹簧仍在弹性限度内)，这时三个小球均静止于距离P足够远的水平轨道上，若撤去外力，C球恰好可运动到轨道的最高点Q，已知重力加速度为g，求撤去外力前的瞬间，弹簧的弹性势能E是多少？

28.(2006年唐山)．(16分)在绕地球做匀速圆周运动的宇宙飞船中，由于失重，因此无法利用天平称出物体的质量。科学家们用下述方法巧妙地测出了一物块的质量。将一带有推进器、总质量m为5kg的小滑车静放在一平台上，平台与小车间的动摩擦因数为0.005，开动推进器，小车在推进器产生的恒力作用下从静止开始运动，测得小车前进1.25m历时5s。关闭推进器，将被测物块固定在小车上，重复上述过程，测得5s内小车前进了1.00m。问：科学家们用上述方法测得的物块的质量M是多少？

27.(2006年3月湖北八校二模)(18分)一宇宙人在太空(万有引力可以忽略不计)玩垒球。如图所示，辽阔的太空球场半侧为匀强电场，另半侧为匀强磁场，电场和磁场的分界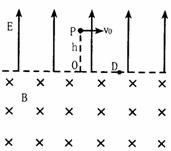面为垂直纸面的平面，电场方向与界面垂直，磁场方向垂直纸面向里，电场强度大小 E = 100V / m 。宇宙人位于电场一侧距界面为 h=3m 的P点，O为P点至界面垂线的垂足，D点位于纸面上O点的右侧，OD与磁场的方向垂直。垒球的质量 m = 0.1kg ，电量 q=一0.05c 。宇宙人从 P 点以初速度 v0 = 10m / s 平行于界面投出垒球，要使垒球第一次通过界面时就击中D点，求：(计算结果保留三位有效数字)

( l ) O、D 两点之间的距离。

( 2 )垒球从抛出到第一次回到 P 点的时间。

计算论述题专项训练(九)答案

9-1．

9-2

9-3、( 1 ) ( 8 分)设垒球在电场中运动的加速度大小为 a ，时间为 t_l , OD = d ，则：

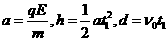　( 6 分，每式 2 分)

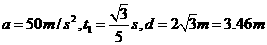　即O、D 两点之间的距离为 3.46m 。( 2 分，没有保留三位有效数字的扣 1 分)

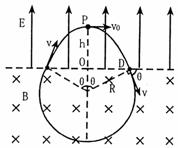
　( 2 ) ( 10 分)垒球的运动轨迹如图所示。

由图可知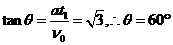， ，速度大小为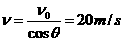： 。( 2 分)

设垒球作匀速圆周运动半径为 R ，　 磁感应强度大小为 B ，

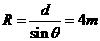　。( 2 分)

根据牛顿第二定律，有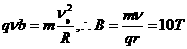： ( 2 分)

垒球在磁场中运动的时间为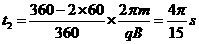： 　( 2 分)

垒球从抛出到第一次回到 P 点的时间为：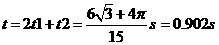

计算论述题专项训练(十)

26.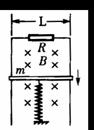(湖北八市2006年3月)(19分)如图所示，固定的竖直光滑金属导轨，间距为L，上端接有阻值为R的电阻，处在方向水平，垂直导轨平面向里的磁感应强度为B的匀强磁场中，质量为m的导体棒的下端与固定竖直弹簧相连且保持与导轨接触良好，导轨与导体棒的电阻均可忽略，弹簧的劲度系数为K，初始时刻，弹簧恰处于自然长度，导体棒具有竖直向下的初速度，动能为E_k,导体棒在沿导轨往复运动的过程中，导体棒始终与导轨垂直。

(1)求初始时刻导体棒受到的安培力。

(2)导体棒往复运动。一段时间后，最终将静止，设棒静止是弹簧的弹性势能为E_p，则从初始时刻到最终金属棒静止的过程中，电阻R上产生的焦耳热Q为多少？

25.(株州2006年3月)设质子的半径为r₀,氢气的摩尔质量为M，阿伏加德罗常数为N₀，万有引力恒量为G，如果在宇宙间有一个恒星的密度等于质子的密度，假想该恒星的第一宇宙速度达到光速C，电子质量忽略不计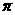，值取3，(计算时，将质子视作球形物体)。求：

(1)　　　　　 该恒星的密度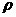；(2)该恒星的半径R；(3)该恒星表面的重力加速度g.