4.如图所示的电路中，1、2、3、4、5、6为连接点的标号。在开关闭合后，发现小灯泡不亮。现用多用电表检查电路故障，需要检测的有：电源、开关、小灯泡、3根

导线以及电路中的各点连接。

(1)为了检测小灯泡以及3根导线，在连接点1、2已接好的情况下，应当选用多用电表的　 　　　挡。在连接点1、2同时断开的情况下，应当选用多用电表的　　 挡。

(2)在开关闭合情况下，若测得5、6两点间的电压接近电源的电动势，则表明___　　 可能有故障

(3)将小灯泡拆离电路，写出用多用表检测该小灯泡是否有故障的具体步骤。

2.图示为简单欧姆表原理示意图，其中电流表的偏电流=300A,内阻R_g=100 ，可变电阻R的最大阻值为10 k，电池的电动势E=1.5 V,内阻r=0.5 ，图中与接线柱A相连的表笔颜色应是　　　　　　 色，接正确使用方法测量电阻R_x的阻值时，指针指在刻度盘的正中央，则R_x=　　　　　　 k.若该欧姆表使用一段时间后，电池电动势变小，内阻变大，但此表仍能调零，按正确使用方法再测上述R_x其测量结果与原结果相比较　　　　　　 (填“变大”、“变小”或“不变”)。3.某研究性学习小组为了制作一种传感器，需要选用一电器元件。图为该电器元件的伏安特性曲线，有同学对其提出质疑，先需进一步验证该伏安特性曲线，实验室备有下列器材：

器材(代号)	规格
电流表(A1) 电流表(A2) 电压表(V1) 电压表(V2) 滑动变阻器(R1) 滑动变阻器(R2) 直流电源(E) 开关(S) 导线若干	量程0~50mA，内阻约为50 量程0~200mA，内阻约为10 量程0~3V，内阻约为10k 量程0~15V，内阻约为25k 阻值范围0~15，允许最大电流1A 阻值范围0~1k，允许最大电流100mA 输出电压6V，内阻不计

①为提高实验结果的准确程度，电流表应选用　　　　 ；电压表应选用　　　　　 ；滑动变阻器应选用　　　　　　　 。(以上均填器材代号)

②为达到上述目的，请在虚线框内画出正确的实验电路原理图，并标明所用器材的代号。

③若发现实验测得的伏安特性曲线与图中曲线基本吻合，请说明该伏安特性曲线与小电珠的伏安特性曲线有何异同点？

相同点：　　　　　　　　　　　　　　　　　　　 ，

不同点：　　　　　　　　　　　　　　　　　　　 。

1.(1)如图甲所示，在“描绘小灯泡的伏安特性曲线”实验中，同组同学已经完成部分导线的连接，请你在实物接线图中完成余下导线的连接。

(2)某同学从标称为“220 V 25 W”、“220 V 500 W”的3只灯泡中任选一只，正确使用多用电表测量灯泡阻值如图乙所示。该灯泡的阻值是___________，标称的额定功率为______________

15.[解析]

m与M之间速度不同，必然存在相对运动，在相互的摩擦力作用下m减速而M加速，当两者速度相同时无相对运动达共速，所以m的最终速度即为两者的共同速度。对m、M整体分析知，系统所受合外力为零，动量守恒，既然两者出现共速，动能必然要减少，从能量守恒的角度看，减少的动能转化为内能产生焦耳热。产生的热就其原因看是由于两者的相互摩擦，所以可以利用摩擦力产生热的特点即得解。

(1)对m、M组成系统受力分析知，其合外力为零，由动量守恒得

　　　　　　　　 　　　　　　　　　　　　　　1

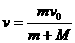　　　　　 ∴　 　　　　　　　　　　　　　　　　　2

　　 (2)对系统由能量守恒得产生焦耳热

　　　　　　　 　　　　　　　　　　3

　　　　　　 ∴　 由2、3解得　　 　　　　　　　4

　　 (3)由滑动摩擦力生热特点得

　　　　　　　 　　　　　　　　　　　　　5

　　　　 ∴　 解得　 　　　　　　　　　　　6

14.[解析]

^{整个过程中，先是变加速运动，接着匀减速，最后匀速运动，作出v-t图线如图(1)所示。由于第一段内作非匀变速直线运动，用常规方法很难求得这1800m位移内的运动时间。考虑动量定理，将第一段的v-t图按比例转化成f-t图，如图(2)所示，则可以巧妙地求得这段时间。}

设变加速下落时间为t₁，

又：mg=kv_m，得　　 所以：

第二段1s内：　　

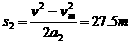
所以第三段时间

空中的总时间：

13.[解析]

解法l　 取物体为研究对象，它的运动可明显分为三个过程。设第一、二两过程末的速度分别为v₁和v₂。，物体所受摩擦力为f，规定推力的方向为正方向。根据动量定理对三个过程分别有：

联立上述三式得　

解法2　 规定推力的方向为正方向，在物体运动的整个过程中，物体的初动量p₁=0，末动量p₂=0。据动量定理有

即：　

解得　

12.[解析]

(1)由机械能守恒定律可得：mgR＝+得　　β＝3

　(2)设A、B碰撞后的速度分别为v₁、v₂，则　　=　　=

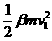设向右为正、向左为负，解得　v₁＝，方向向左　v₂＝，方向向右

设轨道对B球的支持力为N，B球对轨道的压力为N ^/，方向竖直向上为正、向下为负。则　

N－βmg＝βm　　　N ^/＝－N＝－4.5mg，方向竖直向下

(3)设A、B球第二次碰撞刚结束时的速度分别为V₁、V₂，则

解得：V₁＝－，V₂＝0(另一组：V₁＝－v₁，V₂＝－v₂，不合题意，舍去)

由此可得：当n为奇数时，小球A、B在第n次碰撞刚结束时的速度分别与第一次碰撞刚结束时相同；当n为偶数时，小球A、B在第n次碰撞刚结束时的速度分别与第二次碰撞刚结束时相同

11.[解析]

　取水平向左为正方向，冰车、人、球为系统．由动量守恒定律，

对第一次推球过程有：　

对第二次整个接、推球过程有：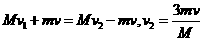

对第三次整个接、推球过程有：

　 对第n次整个接、推球过程同理分析得：　　

设推球n次后恰接不到球，则，故有　 代人已知条件

解得：n = 8.5，　　 即人推球9次后将接不到球．

10.[解析]

(1)设所有物块都相对木板静止时的速度为 v，因木板与所有物块系统水平方向不受外力，动量守恒，应有：

m v+m·2 v+m·3 v+…+m·n v=(M + nm)v　　　 1

　　　　　　 　M = nm，　 　　　　　　　　　　　　　　2

解得:　　　　　 v=(n+1)v，

　　 (2)设第1号物块相对木板静止时的速度为v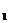，取木板与物块1为系统一部分，第2 号物块到第n号物块为系统另一部分，则

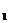　　　 木板和物块1　　 △p =(M + m)v-m v，

　　　 2至n号物块　　 △p=(n-1)m·(v- v)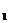

由动量守恒定律： △p=△p，

解得　　　　　 　v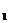= v，　　　　　　　　　　 3

(3)设第k号物块相对木板静止时的速度由v ，则第k号物块速度由k v减为v的过程中，序数在第k号物块后面的所有物块动量都减小m(k v- v)，取木板与序号为1至K号以前的各物块为一部分，则　

△p=(M+km)v-(m v+m·2 v+…+mk v)=(n+k)m v-(k+1)m v

序号在第k以后的所有物块动量减少的总量为

　　 　△p=(n-k)m(k v- v)

由动量守恒得　 △p=△p， 即

(n+k)m v-(k+1)m v= (n-k)m(k v- v)，

解得　　　　 v=

9.[解析]

设人走到船尾时，人的速度为，船的速度为　　　　　　　　　　　　　　　　

　 　对系统分析：动量守恒

　　 对船分析：(匀加速运动) S =　

　　 对人分析：(匀加速运动) 　　

　　　　　　　　　　　　 得：S = 3.25 m.