
题目列表(包括答案和解析)
例3. 图2中,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平直导轨上,弹簧处在原长状态。另一质量与 B相同滑块A,从导轨上的P点以某一初速度向B滑行,当A滑过距离l1时,与B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连。已知最后A恰好返回出发点P并停止,滑块A和B与导轨的滑动摩擦因数都为
B相同滑块A,从导轨上的P点以某一初速度向B滑行,当A滑过距离l1时,与B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连。已知最后A恰好返回出发点P并停止,滑块A和B与导轨的滑动摩擦因数都为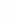 ,运动过程中弹簧最大形变量为l2,重力加速度为g,求A从P出发时的初速度v0。
,运动过程中弹簧最大形变量为l2,重力加速度为g,求A从P出发时的初速度v0。
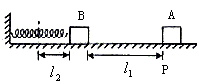
图2
解析:令A、B质量皆为m,A刚接触B时速度为v1(碰前)
由功能关系,有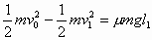
A、B碰撞过程中动量守恒,令碰后A、B共同运动的速度为v2
有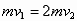
碰后A、B先一起向左运动,接着A、B一起被弹回,在弹簧恢复到原长时,设A、B的共同速度为v3,在这一过程中,弹簧势能始末状态都为零,利用功能关系,有
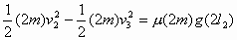
此后A、B开始分离,A单独向右滑到P点停下,由功能关系有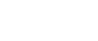
由以上各式,解得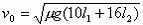
例2. 在原子核物理中,研究核子与核子关联的最有效途径是“双电荷交换反应”。这类反应的前半部分过程和下述力学模型类似,两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态,在它们左边有一垂直于轨道的固定挡板P,右边有一小球C沿轨道以速度v0射向B球,如图1所示,C与B发生碰撞并立即结成一个整体D,在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变,然后,A球与挡板P发生碰撞,碰后A、D都静止不动,A与P接触而不粘连,过一段时间,突然解除锁定(锁定及解除锁定均无机械能损失),已知A、B、C三球的质量均为m。
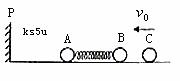
图1
(1)求弹簧长度刚被锁定后A球的速度。
(2)求在A球离开挡板P之后的运动过程中,弹簧的最大弹性势能。
解析:(1)设C球与B球粘结成D时,D的速度为v1,由动量守恒得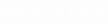 当弹簧压至最短时,D与A的速度相等,设此速度为v2,由动量守恒得
当弹簧压至最短时,D与A的速度相等,设此速度为v2,由动量守恒得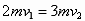 ,由以上两式求得A的速度
,由以上两式求得A的速度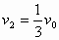 。
。
(2)设弹簧长度被锁定后,贮存在弹簧中的势能为EP,由能量守恒,有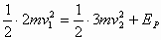 撞击P后,A与D的动能都为零,解除锁定后,当弹簧刚恢复到自然长度时,势能全部转弯成D的动能,设D的速度为v3,则有
撞击P后,A与D的动能都为零,解除锁定后,当弹簧刚恢复到自然长度时,势能全部转弯成D的动能,设D的速度为v3,则有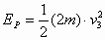
以后弹簧伸长,A球离开挡板P,并获得速度,当A、D的速度相等时,弹簧伸至最长,设此时的速度为v4,由动量守恒得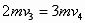
当弹簧伸到最长时,其势能最大,设此势能为EP”,由能量守恒,有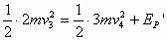 解以上各式得
解以上各式得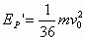 。
。
说明:对弹簧模型来说“系统具有共同速度之时,恰为系统弹性势能最多”。
例1. 在光滑水平地面上有两个相同的弹性小球A、B,质量都为m,现B球静止,A球向B球运动,发生正碰。已知碰撞过程中总机械能守恒,两球压缩最紧时的弹性势能为EP,则碰前A球的速度等于( )
A. 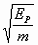 B.
B. 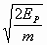 C.
C. 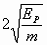 D.
D. 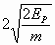
解析:设碰前A球的速度为v0,两球压缩最紧时的速度为v,根据动量守恒定律得出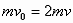 ,由能量守恒定律得
,由能量守恒定律得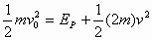 ,联立解得
,联立解得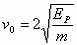 ,所以正确选项为C。
,所以正确选项为C。
与松弛的绳子相连接的物体,在突然被绳子紧拉一下时,其机械能会发生突变,转变为其他形式的能,解这类题目要特别注意,否则将发生一系列连锁错误。
例3. 在光滑水平面上, 有一质量
有一质量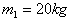 的小车,通过一根几乎不可伸长的轻绳与另一质量
的小车,通过一根几乎不可伸长的轻绳与另一质量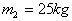 的拖车连接,一质量
的拖车连接,一质量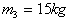 的物体放在拖车的平板上,物体与平板间的动摩擦因数
的物体放在拖车的平板上,物体与平板间的动摩擦因数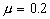 ,开始时,拖车静止,绳未拉紧,如图3所示,小车以
,开始时,拖车静止,绳未拉紧,如图3所示,小车以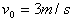 的速度前进,求:
的速度前进,求:
(1) 以同一速度前进时,其速度的大小;
以同一速度前进时,其速度的大小;
(2)物体在拖车平板上移动的距离。
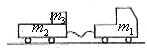
图3
分析与解答:整个运动过程可分成两个阶段:①绳子被拉紧时,m1与m2获得共同速度,m1、m2系统的动量守恒,由于绳子由未绷紧到绷紧,会有机械能的损失(在这个问题上很容易被忽视),此时m3的速度还为零;②绳子拉紧后,在摩擦力作用下m3加速,m1与m2减速,m3与m2间有相对滑动,直至三者速度相等,一起运动。此阶段系统动量守恒,机械能不守恒,但可由动能定理求解。
绳刚被拉紧时,设m1与m2的共同速度为v1,m1与m2系统动量守恒,有:
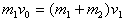
解得: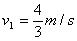
再对m1、m2、m3系统,由动量守恒得:
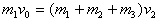
解得: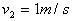
绳拉紧后,物体在拖车上相对滑动,设拖车位移为s1,物体位移为s2,分别对两车、物体用动能定理有:
小车和拖车:
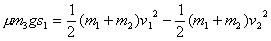
物块: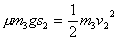
可解得物体在拖车上移动的距离:
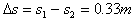
与绳子相连接的物体,由于某些时候绳子的形变发生突变,它的速度会随着发生突变,对这类问题若不加仔细分析,引起注意,接下来其他量的求解就会随着出错,因此必须引起高度重视。
例2. 如图2所示,质量为m的小球用长为L的细绳系于O点,把小球拿到O点正上方且使细绳拉直的位置A后,以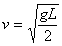 的速度水平向右弹出(空气阻力不计)
的速度水平向右弹出(空气阻力不计)
(1)小球从弹出至下落到与O点等高的位置这一过程中,小球做什么运动,请说明理由;
(2)求小球到达最低点时细绳上的拉力大小。
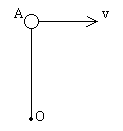
图2
分析与解答:(1)设球在最高点只受重力且做圆周运动,则有:
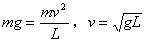
因为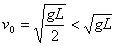 ,所以小球做平抛运动。
,所以小球做平抛运动。
(2)设小球下落到与O点等高的位置时,在水平方向的位移为x,有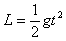 ,
,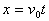 ,得:
,得:
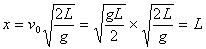
水平方向速度:
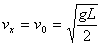
竖直方向的速度:
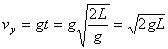
在此,小球在水平方向的速度突变为0,消失了,只剩下竖直向下的速度,此后,小球以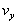 为初速向下做圆周运动(同学们往往在此发生错误)。设小球下落到最低点时速度为
为初速向下做圆周运动(同学们往往在此发生错误)。设小球下落到最低点时速度为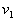 ,绳子拉力为
,绳子拉力为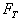 ,由机械能守恒:
,由机械能守恒:
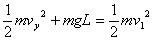
又由牛顿第二定律有:
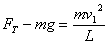
解得: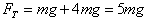
由于绳子的特点,它的弹力可发生突变,它与弹簧不同,弹簧的弹力不能发生突变,同学们一定要注意区别,不能混淆。
例1. 如图1所示,一条轻弹簧OB和一根细绳OA共同拉住一个质量为m的小球,平衡时细绳OA是水平的,弹簧与竖直方向的夹角是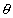 ,若突然剪断细绳OA,则在刚剪断的瞬间,弹簧拉力的大小是_________,小球加速度的方向与竖直方向的夹角等于_________,若将弹簧改为一根细绳,则在OA线剪断瞬间,绳OB的弹力大小是________,小球加速度方向与竖直方向夹角等于__________。
,若突然剪断细绳OA,则在刚剪断的瞬间,弹簧拉力的大小是_________,小球加速度的方向与竖直方向的夹角等于_________,若将弹簧改为一根细绳,则在OA线剪断瞬间,绳OB的弹力大小是________,小球加速度方向与竖直方向夹角等于__________。
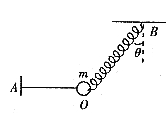
图1
分析与解答:这是一道典型的要区分细绳与弹簧有什么不同的题,只要我们认清细绳可发生突变,而弹簧不能发生突变的情况,则这就不是一道难题。
细绳未剪断前,小球所受重力,弹簧的拉力和细绳的拉力是平衡的,即重力与弹簧的拉力的合力是沿水平方向向右,大小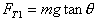 ,细绳剪断后,弹簧的形变不能马上改变,弹力仍保持原值
,细绳剪断后,弹簧的形变不能马上改变,弹力仍保持原值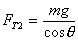 ,因重力、弹簧弹力不变,所以此时小球加速度方向是沿水平向右,即与竖直方向夹角是
,因重力、弹簧弹力不变,所以此时小球加速度方向是沿水平向右,即与竖直方向夹角是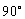 ,若弹簧改用细绳,则OA线剪断瞬间,细绳OB的形变发生突变,小球有沿圆弧切线方向的加速度,故重力与绳OB的拉力的合力必沿切线方向,由此求得
,若弹簧改用细绳,则OA线剪断瞬间,细绳OB的形变发生突变,小球有沿圆弧切线方向的加速度,故重力与绳OB的拉力的合力必沿切线方向,由此求得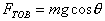 ,夹角为
,夹角为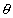 。
。
5.
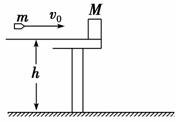 (2008年高考全国卷Ⅱ)如图6-3-12所示,一质量为M的物块静止在桌面边缘,桌面离水平地面的高度为h.一质量为m的子弹以水平速度v0射入物块后,以水平速度v0/2射出.重力加速度为g.求:
(2008年高考全国卷Ⅱ)如图6-3-12所示,一质量为M的物块静止在桌面边缘,桌面离水平地面的高度为h.一质量为m的子弹以水平速度v0射入物块后,以水平速度v0/2射出.重力加速度为g.求:
(1)此过程中系统损失的机械能;
(2)此后物块落地点离桌面边缘的水平距离.
解析:(1)设子弹穿过物块后物块的速度为v,由动量守恒得mv0=m+Mv① www.k@s@5@ 高#考#资#源#网
解得v=v0②
系统的机械能损失为
ΔE=mv02-[m()2+Mv2]③
由②③式得ΔE=(3-)mv02.④
(2)设物块下落到地面所需时间为t,落地点距桌面边缘的水平距离为s,则h=gt2⑤
s=vt⑥
由②⑤⑥式得s=.
答案:(1)(3-)mv02 (2)
4.
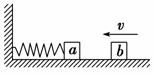 如图6-3-11所示,在光滑水平面上有质量分别为3m和m的a、b两物体,a与轻弹簧一端相连,弹簧的另一端固定在墙上.开始弹簧处于原长,b以速度v与a发生正碰,碰后两物体以相同速度压缩弹簧,当弹簧被压缩到最短时,它具有的弹性势能为( )
如图6-3-11所示,在光滑水平面上有质量分别为3m和m的a、b两物体,a与轻弹簧一端相连,弹簧的另一端固定在墙上.开始弹簧处于原长,b以速度v与a发生正碰,碰后两物体以相同速度压缩弹簧,当弹簧被压缩到最短时,它具有的弹性势能为( )
A.mv2/2 B.mv2/8
C.mv2/4 D.mv2/16
解析:选B.a、b发生正碰,获得共速v共,由动量守恒:mv=(m+3m)v共,然后以v共去压缩弹簧,由机械能守恒:Ep=(m+3m)v共2/2,联立解得Ep=mv2/8
3.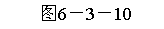
 如图6-3-10所示,质量为M、长为L的长木板放在光滑水平面上,一个质量也为M的物块(视为质点)以一定的初速度从左端冲上木板,如果长木板是固定的,物块恰好停在木板的右端,如果长木板不固定,则物块冲上后在木板上最多能滑行的距离为( )
如图6-3-10所示,质量为M、长为L的长木板放在光滑水平面上,一个质量也为M的物块(视为质点)以一定的初速度从左端冲上木板,如果长木板是固定的,物块恰好停在木板的右端,如果长木板不固定,则物块冲上后在木板上最多能滑行的距离为( )
A.L B.3L/4
C.L/4 D.L/2
解析:选D.固定时,由动能定理得:μMgL=Mv02,后来木板不固定有Mv0=2Mv,μMgs=Mv02-·2Mv2,故得s=L/2.
2.
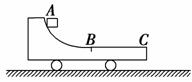 (2009年宜昌模拟)如图6-3-9所示,小车M由光滑的弧形段AB和粗糙的水平段BC组成,静止在光滑水平面上.当小车固定时,从A点由静止滑下的物块m到C点恰好停止.如果小车不固定,物块m仍从A点静止滑下,( )
(2009年宜昌模拟)如图6-3-9所示,小车M由光滑的弧形段AB和粗糙的水平段BC组成,静止在光滑水平面上.当小车固定时,从A点由静止滑下的物块m到C点恰好停止.如果小车不固定,物块m仍从A点静止滑下,( )
A.还是滑到C点停住 B.滑到BC间某处停住
C.会冲出C点落到车外 D.上述三种情况都有可能
解析:选A.小车固定时恰能滑到C点,机械能会全部转化为内能.当小车不固定时,由动量守恒知,小车与物体的最终速度都为零,故机械能全部转化为内能,因此两次滑过的路程相等,所以A对.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com