3．如图3所示的电路中，两根光滑金属导轨平行放置在倾角

　 为θ的斜面上，导轨下端接有电阻R，导轨电阻不计，斜面

　 处在竖直向上的磁感应强度为B的匀强磁场中，电阻可略去

　 不计的金属棒ab质量为m，受到沿斜面向上且与金属棒垂

　 直的恒力F的作用，金属棒沿导轨匀速下滑，则它在下滑h高度的过程中，以下说

　 法正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

　 A．作用在金属棒上各力的合力做功为零

　 B．重力做功将机械能转化为电能

　 C．重力与恒力F做功的代数和等于电阻R上产生的焦耳热

　 D．金属棒克服安培力做功等于重力与恒力F做的总功与电阻R上产生的焦耳热

　　 之和

　 解析：由于金属棒匀速下滑，故作用在棒上的各个力的合力做功为零，故A对；克

　 服安培力做功将机械能转化为电能，故B错误；列出动能定理方程W_G－W_F－W_安

 ＝0，变形可得W_G－W_F＝W_安，可知C正确，D错误．

　 答案：AC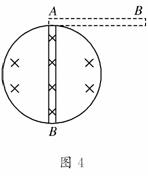

2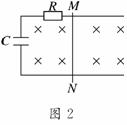．如图2所示，两光滑平行金属导轨间距为L，直导线MN

　 垂直跨在导轨上，且与导轨接触良好，整个装置处于垂直

　 纸面向里的匀强磁场中，磁感应强度为B.电容器的电容

　 为C，除电阻R外，导轨和导线的电阻均不计．现给导线

　 MN一初速度，使导线MN向右运动，当电路稳定后，

　 MN以速度v向右做匀速运动，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 (　)

　 A．电容器两端的电压为零

　 B．电阻两端的电压为BLv

　 C．电容器所带电荷量为CBLv

　 D．为保持MN匀速运动，需对其施加的拉力大小为

　 解析：当导线MN匀速向右运动时，导线MN产生的感应电动势恒定，稳定后，电

　 容器既不充电也不放电，无电流产生，故电阻两端无电压，电容器两极板间电压U

　 ＝E＝BLv，所带电荷量Q＝CU＝CBLv，故A、B错，C对；MN匀速运动时，因

　 无电流而不受安培力，故拉力为零，D错．

　 答案：C

7分，选对但不全的得4分，有选错的得0分)

1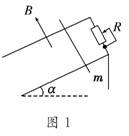．(2010·宁波模拟)如图1所示，有两根和水平方向成α角的光

　 滑平行的金属轨道，上端接有可变电阻R，下端足够长，空间

　 有垂直于轨道平面的匀强磁场，磁感应强度为B.一根质量为m

　 的金属杆从轨道上由静止滑下，经过足够长的时间后，金属杆

　 的速度会趋近于一个最大速度v_m，则　　　　　 　(　)

　 A．如果B增大，v_m将变大

　 B．如果α变大，v_m将变大

　 C．如果R变大，v_m将变大

　 D．如果m变小，v_m将变大

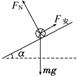
　 解析：以金属杆为研究对象，受力如图所示．

　 根据牛顿第二定律得

　 mgsinα－F_安＝ma，其中F_安＝.

　 当a→0时，v→v_m，

　 解得v_m＝，

　 结合此式分析即得B、C选项正确．

　 答案：BC

0．5－＝0

代入数据得：B＝0.5 T.

(3)设外力F作用时间为t.x₁＝at²

v₀＝x₂＝at

x₁+x₂＝s，所以at²+at＝s

代入数据得0.2t²+0.8t－1＝0，

解方程得t＝1 s或t＝－5 s(舍去)．

(4)可能图线如下：

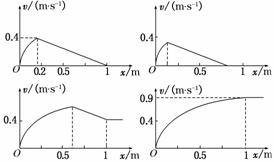
答案：(1)见解析　(2)0.5 T　(3)1 s　(4)见解析

16．(12分)(2009·上海高考)如图17所示，光滑的平行金属导轨水平放置，电阻不计，

导轨间距为l，左侧接一阻值为R的电阻．区域cdef内存在垂直轨道平面向下的有

界匀强磁场，磁场宽度为s.一质量为m、电阻为r的金属棒MN置于导轨上，与导

轨垂直且接触良好，受到F＝0.5v+0.4(N)(v为金属棒速度)的水平外力作用，从磁场

的左边界由静止开始运动，测得电阻两端电压随时间均匀增大．(已知：l＝1 m，m

＝1 kg，R＝0.3 Ω，r＝0.2 Ω，s＝1 m)

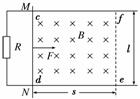
图17

(1)分析并说明该金属棒在磁场中做何种运动；

(2)求磁感应强度B的大小；

(3)若撤去外力后棒的速度v随位移x的变化规律满足v＝v₀－x，且棒在运动

到ef处时恰好静止，则外力F作用的时间为多少？

(4)若在棒未出磁场区域时撤出外力，画出棒在整个运动过程中速度随位移变化所对

应的各种可能的图线．

解析：(1)金属棒做匀加速直线运动

R两端电压U∝I∝E∝v，U随时间均匀增大，即v随时间均匀增大．

所以加速度为恒量．

(2)F－v＝ma，将F＝0.5v+0.4代入

得：(0.5－)v+0.4＝a

因为加速度为恒量，与v无关，所以a＝0.4 m/s²

15．(10分)如图16所示，竖直放置的等距离金属导轨宽0.5 m，垂直于导轨平面向里

的匀强磁场的磁感应强度为B＝4 T，轨道光滑、电阻不计，ab、cd为两根完全相同

的金属棒，套在导轨上可上下自由滑动，每根金属棒的电阻为1 Ω.今在ab棒上施加

一个竖直向上的恒力F，这时ab、cd恰能分别以0.1 m/s的速度向上和向下做匀速滑

行．(g取10 m/s²)试求：

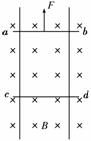
图 16

(1)两棒的质量；

(2)外力F的大小．

解析：(1)根据右手定则，可以判定电路中电流方向是沿acdba流动的．设ab棒的质

量为m₁，cd棒的质量为m₂.取cd棒为研究对象，受力分析，根据平衡条件可得BIL

＝m₂g

其中I＝＝，得m₂＝＝0.04 kg，

根据题意判断可知m₁＝0.04 kg.

(2)取两根棒整体为研究对象，根据平衡条件可得

F＝m₁g+m₂g＝0.8 N.

答案：(1)0.04 kg　0.04 kg　(2)0.8 N

14．(9分)一根电阻R＝0.6 Ω的导线弯成一个圆形线圈，圆半径r＝1 m，圆形线圈质

量m＝1 kg，此线圈放在绝缘光滑的水平面上，在y轴右侧有垂直线圈平面的磁感应

强度B＝0.5 T的匀强磁场，如图15所示．若线圈以初动能E₀＝5 J沿x轴方向滑进

磁场，当进入磁场0.5 m时，线圈中产生的电能为E＝3 J．求：

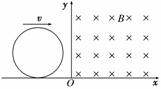
图15

(1)此时线圈的运动速度的大小；

(2)此时线圈与磁场左边缘两交接点间的电压；

(3)此时线圈加速度的大小．

解析：(1)设线圈的速度为v，由能量守恒定律得

E₀＝E+mv².

解得：v＝2 m/s.

(2)线圈切割磁感线的有效长度

L＝2 ＝ m，

电动势E＝BLv＝ V，

电流I＝＝ A，

两交接点间的电压

U＝IR₁＝×0.6× V＝ V.

(3)F＝ma＝BIL，所以a＝2.5 m/s².

答案：(1)2 m/s　(2) V　(3)2.5 m/s²

算步骤，有数值计算的要注明单位)

13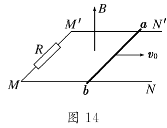．(9分)(2010·宣武模拟)如图14所示，光滑的U形金

属导轨MNN′M′水平的固定在竖直向上的匀强磁

场中，磁感应强度为B，导轨的宽度为L，其长度足

够长，M′、M之间接有一个阻值为R的电阻，其

余部分电阻不计．一质量为m、电阻也为R的金属

棒ab恰能放在导轨之上，并与导轨接触良好．给棒

施加一个水平向右的瞬间作用力，棒就沿轨道以初速度v₀开始向右滑行．求：

(1)开始运动时，棒中的瞬时电流i和棒两端的瞬时电压u分别为多大？

(2)当棒的速度由v₀减小到v₀/10的过程中，棒中产生的焦耳热Q是多少？

解析：(1)开始运动时，棒中的感应电动势：

E＝BLv₀

棒中的瞬时电流：i＝＝

棒两端的瞬时电压：u＝E＝BLv₀.

(2)由能量守恒定律知，闭合电路在此过程中产生的焦耳热：Q_总＝mv₀²－m(v₀)²

＝mv₀²

棒中产生的焦耳热为：Q＝Q_总＝mv₀².

　 答案：(1)　BLv₀　(2)mv₀²

12．如图12所示，在PQ、QR区域中存在着磁感应强度大小相等、方向相反的匀强磁

场，磁场方向均垂直于纸面．一导线框abcdefa位于纸面内，框的邻边都相互垂直，

bc边与磁场的边界P重合．导线框与磁场区域的尺寸如图所示．从t＝0时刻开始，

线框匀速横穿两个磁场区域．以a→b→c→d→e→f为线框中的电动势E的正方向，

则如图13所示的四个E－t关系示意图中正确的是　　　　　　　　　　　　　　　　　　　 (　)

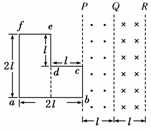
图12

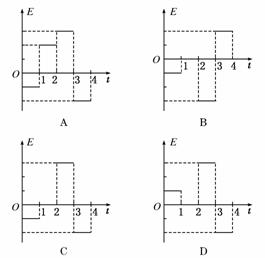
图13

解析：由右手定则和E＝Blv判定水平位移从0-l时E＝Blv；从l-2l时，E＝0；

从2l-3l时，E＝3Blv；从3l-4l时，E＝－2Blv，可知图C正确．

　 答案：C

11．如图11所示，两根水平放置的相互平行的金属导轨ab、

cd，表面光滑，处在竖直向上的匀强磁场中，金属棒PQ

垂直于导轨放在上面，以速度v向右匀速运动，欲使棒

PQ停下来，下面的措施可行的是(导轨足够长，棒PQ有

电阻)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．在棒PQ右侧垂直于导轨再放上一根同样的金属棒

B．在棒PQ棒右侧垂直于导轨再放上一根质量和电阻均比棒PQ大的金属棒

C．将导轨的a、c两端用导线连接起来

D．将导轨的a、c两端和b、d两端分别用导线连接起来

解析：在棒PQ右侧放金属棒时，回路中会有感应电流，使金属棒加速，棒PQ减速，

当两者获得共同速度时，回路中感应电流为零，两棒都将做匀速运动，A、B项错误．当

一端或两端用导线连接时，棒PQ的动能将转化为内能而最终静止，C、D两选项

正确．

答案：CD