
题目列表(包括答案和解析)
1、如图所示的圆盘中三个扇形大小相同,则指针落在黄区域的概率是( )
A、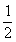 B、
B、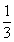 C、
C、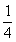 D、
D、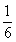
8、小明和爸爸进行射击比赛,他们每人都射击10次。小明击中靶心的概率为0.6,则他击不中靶心的次数为 ;爸爸击中靶心8次,则他击不中靶心的概率为 。
7、一只口袋中有4只红球和5个白球,从袋中任摸出一个球,则P(抽到红球) P(抽到白球)(填“>”或“<”)。
6、某中学学生情况如右表:
若任意抽取一名该校的学生,是高中生的概率是 ;是女生的概率是 。
5、轰炸机练习空中投靶,靶子是在空地上的一个巨型正方形铁板,板上画有大小相同的36个小正方形,其中6个红色,30个黑色,那么投中红色小正方形的概率为 。
|
|
高中(人) |
初中(人) |
|
女生 |
200 |
450 |
|
男生 |
500 |
850 |
4、学校升旗要求学生穿校服,但有一些粗心大意的学生忘记了,若500名学生中没有穿校服的学生为25名,则任意叫出一名学生,没穿校服的概率为 ;穿校服的概率为 。
3、有一组卡片,制作的颜色,大小相同,分别标有0~10这11个数字,现在将它们背面向上任意颠倒次序,然后放好后任取一组,则:
(1)P(抽到两位数)= ;
(2)P(抽到一位数)= ;
(3)P(抽到的数是2的倍数)= ;
(4)P(抽到的数大于10)= ;
2、一般地,就事件发生的可能性而言,可将事件分为 、
和 。
1、游戏的公平性是指双方获胜的概率 。
(二)解答题:
1、如图,已知AB=AC,AD是BC边上的中线,你能说明AD是角平分线吗?
证明:∵AD是BC边上的中线(已知)
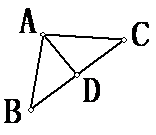 ∴ = (中线的定义)
∴ = (中线的定义)
在 中
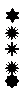
∴ ≌ ( )
∴ = (全等三角形的对应角相等)
∴AD是角平分线( )
2、如图,已知AB=AC,AE=AD,∠1=∠2,你能说明△ABD≌△ACE吗?
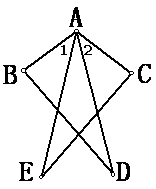
3、如图,要量河两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直线上,这时测得DE的长就是AB的长,试说明理由。
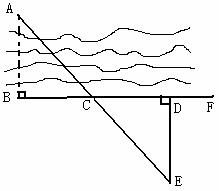
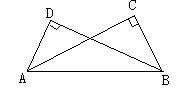
4、如图,AD=BC,∠D=∠C=90°,△ABD和△BAC全等吗?
5、尺规作图:(1)已知三角形的两角及其夹边,求作这个三角形.
已知:线段∠α,∠β,线段a 。
求作:ΔABC,使得∠A=∠α,∠B=∠β,AB=a。

(2) 已知三角形的两边及其夹角,求作这个三角形.
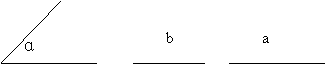 已知:
已知:
求作:
7、请用全等图形设计一个你自己认为满意的图案。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com