6.如图所示，已知在△ABC中，∠BAC＝70°，AC=6，AD是△ABC的角平分线，则∠BAD=　　　　 。BE是△ABC的中线，则AE=CE=　　　　　 ，CF是△ABC的高，

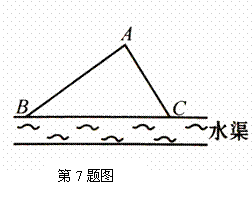则∠　　　 =∠　　　　 =90°.

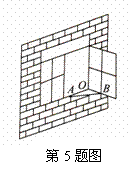
5.如图所示，一扇窗户打开后，用窗钩AB可将其固定，这里所用的几何原理是(　　 )

A.三角形的稳定性　　　 B.两点之间线段最短　　 C.两点确定一直线　　　 D.垂线段最短

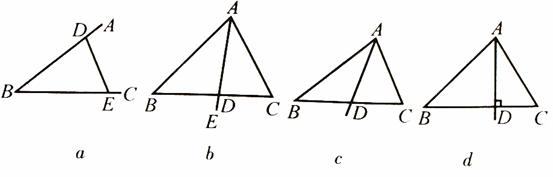
4.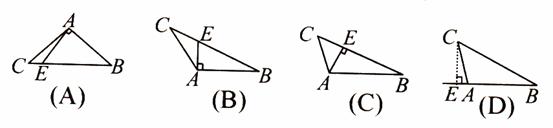下列说法中正确的是(　　　 )

A.如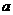，由AB、BC、DE三条线段组成的图形是三角形

B.如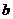，已知∠BAD＝∠CAD，则射线AD是△ABC的角平分线

C.如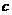，已知D为BC的中点，则线段AE为△ABC的中线

D.如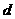，已知△ABC中，AD⊥BC交于点D，则线段AD是△ABC的高

3.下图中AE是△ABC的高线，作图正确的是(　　　 )

2.如果三角形三条高的交点是三角形的一个顶点，那么这个三角形是(　　　 )

A.锐角三角形　　 B.钝角三角形　　 C.直角三角形　　 D. 以上说法都不正确

1. 1.三角形的角平分线、高和中线均为(　　　 )

A.直线　　 B.射线　　 C.线段　　　　 D.以上说法都不正确

9.解：(1)5长为底边时，设腰长为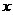，由题意，得2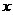+5=21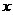，∴=8

(2)5长为腰长时，设底边长为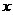，由题意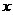，+5×2=2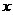1，∴=11.

∵5+5＜11，所以. 5的边不能为腰.

从而可得这个三角形其他两边长为都是7.

第二课时7.1.2三角形的高、中线与角平分线7.1.3三角形的稳定性

8. 8.3、4或3.5、3.5，提示：已知的这边可能为腰即两外两边分别为3，4；当已知的这边为底边时，腰长为3.5，3.5；

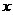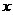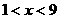1.沿大道3，大道1，2，3组成的三角形中，任意两边之和大于第三边；2.D，提示：依据三角形的三边关系，符合条件的只有D；3.D，提示：依据三角形的三边关系即4+5＞，5-4＜，，所以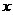的值可能是3，5，7，但不能是9，故选D；4.B，提示：分情况讨论：若腰长为2，两腰长之和为4小于5，而三角形任意之和要大于第三边，所以这种情况不成立；若腰长为5时，两腰长之和为5+5＞2，符合三角形三边关系故当腰长是5，底边为2时周长为5+5+2=12，选B；5.C，提示：.先确定四条线段中，其中三条线段为一组有几种情况，再根据三角形的三边关系判断有哪几组可组成三角形即有13、10、5，13、10、7，10、5、7但13、7、5不成立故有3组选C；6. 6个；△ABD，△ABE，△ABC，△ADE，△ADC，△AEC；7.3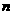+1，提示：图1中4=3×1+1，图2中，7=3×2+1，图3中，10=3×3+1，……第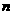个图形中，互不重叠的三角形共有3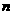+1；

9. 一个等腰三角形的周长为21，一边长为5，求其他两边长.

第一课时答案：