
题目列表(包括答案和解析)
 ="(cosα," sinα), b="(cosβ," sinβ),且
="(cosα," sinα), b="(cosβ," sinβ),且 与b之间满足关系:|k
与b之间满足关系:|k +b|=
+b|=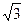 |
| -kb|,其中k>0.
-kb|,其中k>0.  与b的数量积用k表示的解析式f(k);
与b的数量积用k表示的解析式f(k); 能否和b垂直?
能否和b垂直? 能否和b平行?若不能,则说明理由;若能,则求出对应的k值;
能否和b平行?若不能,则说明理由;若能,则求出对应的k值; 与b夹角的最大值。
与b夹角的最大值。已知椭圆
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(I)求椭圆 的方程;
的方程;
(II)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设 为椭圆上一点,且满足
为椭圆上一点,且满足 (O为坐标原点),当
(O为坐标原点),当 <
< 时,求实数
时,求实数 的取值范围.
的取值范围.
【解析】本试题主要考查了椭圆的方程以及直线与椭圆的位置关系的运用。
第一问中,利用
第二问中,利用直线与椭圆联系,可知得到一元二次方程中 ,可得k的范围,然后利用向量的
,可得k的范围,然后利用向量的 <
< 不等式,表示得到t的范围。
不等式,表示得到t的范围。
解:(1)由题意知

已知中心在坐标原点,焦点在 轴上的椭圆C;其长轴长等于4,离心率为
轴上的椭圆C;其长轴长等于4,离心率为 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点 (0,1), 问是否存在直线
(0,1), 问是否存在直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ?若存在,求出
?若存在,求出 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【解析】本试题主要考查了椭圆的方程的求解,直线与椭圆的位置关系的运用。
第一问中,可设椭圆的标准方程为
则由长轴长等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求椭圆C的标准方程为
第二问中,
假设存在这样的直线 ,设
,设 ,MN的中点为
,MN的中点为
因为|ME|=|NE|所以MN EF所以
EF所以
(i)其中若 时,则K=0,显然直线
时,则K=0,显然直线 符合题意;
符合题意;
(ii)下面仅考虑 情形:
情形:
由 ,得,
,得,
 ,得
,得
代入1,2式中得到范围。
(Ⅰ) 可设椭圆的标准方程为
则由长轴长等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求椭圆C的标准方程为
(Ⅱ) 假设存在这样的直线 ,设
,设 ,MN的中点为
,MN的中点为
因为|ME|=|NE|所以MN EF所以
EF所以
(i)其中若 时,则K=0,显然直线
时,则K=0,显然直线 符合题意;
符合题意;
(ii)下面仅考虑 情形:
情形:
由 ,得,
,得,
 ,得
,得 ……② ……………………9分
……② ……………………9分
则 .
.
代入①式得,解得 ………………………………………12分
………………………………………12分
代入②式得 ,得
,得 .
.
综上(i)(ii)可知,存在这样的直线 ,其斜率k的取值范围是
,其斜率k的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com