
题目列表(包括答案和解析)
(1) 以直角坐标系的原点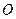 为极点,
为极点,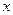 轴的正
轴的正 半轴为极
半轴为极 轴。已知点
轴。已知点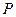 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点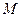 的极坐标为
的极坐标为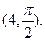 若直线
若直线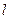 过点
过点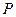 ,且倾斜角为
,且倾斜角为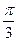 ,圆
,圆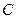 以
以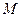 为圆心、
为圆心、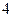 为半径。(I)求直线
为半径。(I)求直线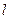 的参数方程和圆
的参数方程和圆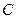 的极坐标方程;(II)试判定直线
的极坐标方程;(II)试判定直线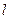 和圆
和圆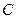 的位置关系.
的位置关系.
(2)把曲线 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于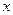 轴的反射变换变为曲线
轴的反射变换变为曲线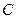 ,求曲线
,求曲线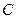 的方程.
的方程.
(3)关于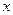 的一元二次方程
的一元二次方程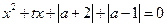 对任意
对任意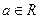 无实根,求实数
无实根,求实数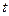 的取值范围.
的取值范围.
已知函数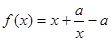
(I)若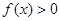 对任意
对任意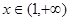 恒成立,求实数
恒成立,求实数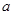 的取值范围;
的取值范围;
(II)解关于x的不等式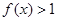 .
.
(1) 以直角坐标系的原点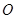 为极点,
为极点,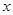 轴的正
轴的正 半轴为极
半轴为极 轴。已知点
轴。已知点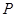 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点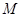 的极坐标为
的极坐标为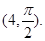 若直线
若直线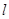 过点
过点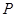 ,且倾斜角为
,且倾斜角为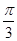 ,圆
,圆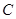 以
以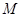 为圆心、
为圆心、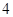 为半径。(I)求直线
为半径。(I)求直线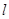 的参数方程和圆
的参数方程和圆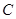 的极坐标方程;(II)试判定直线
的极坐标方程;(II)试判定直线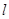 和圆
和圆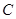 的位置关系.
的位置关系.
(2)把曲线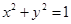 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于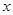 轴的反射变换变为曲线
轴的反射变换变为曲线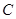 ,求曲线
,求曲线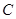 的方程.
的方程.
(3)关于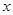 的一元二次方程
的一元二次方程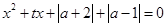 对任意
对任意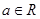 无实根,求实数
无实根,求实数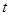 的取值范围.
的取值范围.
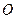 为极点,
为极点,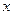 轴的正
轴的正 半轴为极
半轴为极 轴。已知点
轴。已知点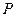 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点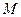 的极坐标为
的极坐标为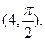 若直线
若直线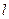 过点
过点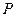 ,且倾斜角为
,且倾斜角为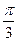 ,圆
,圆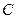 以
以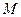 为圆心、
为圆心、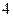 为半径。(I)求直线
为半径。(I)求直线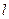 的参数方程和圆
的参数方程和圆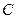 的极坐标方程;(II)试判定直线
的极坐标方程;(II)试判定直线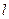 和圆
和圆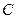 的位置关系.
的位置关系.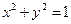 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于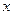 轴的反射变换变为曲线
轴的反射变换变为曲线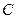 ,求曲线
,求曲线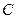 的方程.
的方程.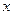 的一元二次方程
的一元二次方程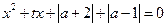 对任意
对任意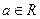 无实根,求实数
无实根,求实数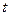 的取值范围.
的取值范围.
已知函数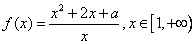 。
。
(I)若对任意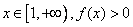 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(II)若对任意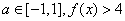 恒成立,求实数x的取值范围。
恒成立,求实数x的取值范围。
一.选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
B
A
C
D
D
D
A
B
A
A
二.填空题
13.4; 14.  ; 15.15; 16.
; 15.15; 16. ,
, 可以填写任一实数.
可以填写任一实数.
三.解答题
17. (Ⅰ)列表:


2
6
10
14

0





1
3
1

1
描点作图,得图象如下.
 6分
6分
(Ⅱ)

所以,当 ,即
,即 时,函数
时,函数 取得最小值
取得最小值 .
12分
.
12分
18.由图可知,参加活动1次、2次和3次的学生人数分别为5、25和20.
(I)该班学生参加活动的人均次数为 =
= . 6分
. 6分
(II)从该班中任选两名学生,他们参加活动次数恰好相等的概率为 .
12分
.
12分
19.(Ⅰ)∵AD=2AB=2,E是AD的中点,
∴△BAE,△CDDE是等腰直角三角形,
易知,∠BEC=90°,即BE⊥EC
又∵平面D′EC⊥平面BEC,面D′EC∩面BEC=EC,
∴BE⊥面D′EC,又CD′ 面D′EC,∴BE⊥CD′.
6分
面D′EC,∴BE⊥CD′.
6分
(Ⅱ)法一:设M是线段EC的中点,过M作MF⊥BC
垂足为F,连接D′M,D′F,则D′M⊥EC
∵平面D′EC⊥平面BEC,
 ∴D′M⊥平面EBC,
∴D′M⊥平面EBC,
∴MF是D′F在平面BEC上的射影,
由三垂线定理得:D′F⊥BC
∴∠D′FM是二面D′―BC―E的平面角.
在Rt△D′MF中,
∴ ,
,
即二面角D′―BC―E的正切值为 .
12分
.
12分
法二:如图,以EB,EC为x轴,y轴,过E垂直于平面BEC的射线为z轴,建立空间直角坐标系,
则
设平面BEC的法向量为 ;平面D′BC的法向量为
;平面D′BC的法向量为


由
取
∴

∴二面角D′―BC―E的正切值为 .
12分
.
12分
20.(I) ,
,

(II) 由(I)知
由(I)知


21(Ⅰ)设椭圆C的方程为 ,则由题意知b = 1.
,则由题意知b = 1.

∴椭圆C的方程为  …………………………………………………6分
…………………………………………………6分
(Ⅱ)易知直线 的斜率为
的斜率为 ,从而直线
,从而直线 的斜率为1.设直线的方程为
的斜率为1.设直线的方程为 ,代如椭圆的方程,并整理可得
,代如椭圆的方程,并整理可得 .设
.设 ,则
,则 ,
, .于是
.于是


解之得 或
或 .
.
当 时,点
时,点 即为直线
即为直线 与椭圆的交点,不合题意.当
与椭圆的交点,不合题意.当 时,经检验知
时,经检验知 和椭圆相交,符合题意.
和椭圆相交,符合题意.
所以,当且仅当直线 的方程为
的方程为 时, 点
时, 点 是
是 的垂心. 12分
的垂心. 12分
22.(Ⅰ)对一切 有
有

于是, 

 (
( ) 5分
) 5分
(Ⅱ)由 及
及
两式相减,得: 


∴ . 10分
. 10分
(Ⅲ) 由于 ,
,
所以, 14分
14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com