
题目列表(包括答案和解析)
已知向量 ,且
,且 ,A为锐角,求:
,A为锐角,求:
(1)角A的大小;
(2)求函数 的单调递增区间和值域.
的单调递增区间和值域.
【解析】第一问中利用 ,解得
,解得 又A为锐角
又A为锐角

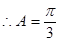
第二问中,
由 解得单调递增区间为
解得单调递增区间为
解:(1) ……………………3分
……………………3分
 又A为锐角
又A为锐角

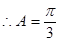 ……………………5分
……………………5分
(2)
……………………8分
由 解得单调递增区间为
解得单调递增区间为
……………………10分

求曲线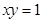 及直线
及直线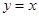 ,
,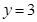 所围成的平面图形的面积.
所围成的平面图形的面积.
【解析】本试题主要是考查了定积分的运用。
解:做出曲线xy=1及直线y=x,y=3的草图,则所求面积为阴影部分的面积
解方程组 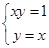 得直线y=x与曲线xy=1的交点坐标为(1,1)
得直线y=x与曲线xy=1的交点坐标为(1,1)
同理得:直线y=x与曲线y=3的交点坐标为(3,3)
直线y=3与曲线xy=1的交点坐标为(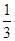 ,3)………………3分
,3)………………3分
因此,所求图形的面积为
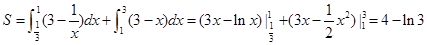
 某大学高等数学老师上学期分别采用了A,B两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如图:
某大学高等数学老师上学期分别采用了A,B两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如图:| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(本小题满分12分)
某大学高等数学老师上学期分别采用了 两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如下:
两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如下:

(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)从乙班这20名同学中随机抽取两名高等数学成绩不得低于85分的同学,求成绩为90分的同学被抽中的概率;
(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
|
|
甲班 |
乙班 |
合计 |
|
优秀 |
|
|
|
|
不优秀 |
|
|
|
|
合计 |
|
|
|
下面临界值表仅供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: 其中
其中 )
)
(Ⅳ)从乙班高等数学成绩不低于85分的同学中抽取2人,成绩不低于90分的同学得奖金100元,否则得奖金50元,记 为这2人所得的总奖金,求
为这2人所得的总奖金,求 的分布列和数学期望。
的分布列和数学期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com