2,4,6
二、填空题:
13、.files/image265.gif) 14、
14、.files/image267.gif) 15、75 16、
15、75 16、.files/image269.gif) 17、② 18、④ 19、
17、② 18、④ 19、.files/image271.gif)
20、.files/image273.gif) 21、
21、.files/image275.gif) 22、
22、.files/image277.gif) 23、
23、.files/image024.gif) 24、
24、.files/image280.gif) 25、
25、.files/image282.gif)
26、.files/image284.gif)
三、解答题:
27解:(1)当.files/image183.gif) 时,
时,.files/image287.gif) ,
,
∵.files/image289.gif)
.files/image291.gif) ,∴
,∴.files/image185.gif) 在
在.files/image187.gif) 上是减函数.
上是减函数.
(2)∵.files/image189.gif) 不等式
不等式.files/image191.gif) 恒成立,即
恒成立,即.files/image189.gif) 不等式
不等式.files/image298.gif) 恒成立,
恒成立,
∴.files/image189.gif) 不等式
不等式.files/image301.gif) 恒成立. 当
恒成立. 当.files/image303.gif) 时,
时,.files/image189.gif)
.files/image306.gif) 不恒成立;
不恒成立;
当.files/image308.gif) 时,
时,.files/image189.gif) 不等式
不等式.files/image301.gif) 恒成立,即
恒成立,即.files/image312.gif) ,∴
,∴.files/image314.gif) .
.
当.files/image316.gif) 时,
时,.files/image189.gif) 不等式
不等式.files/image319.gif) 不恒成立. 综上,
不恒成立. 综上,.files/image193.gif) 的取值范围是
的取值范围是.files/image322.gif) .
.
28解:(1)
.files/image324.gif)
.files/image326.gif)
.files/image328.gif)
.files/image326.gif)
.files/image330.gif)
.files/image326.gif)
.files/image332.gif)
(2).files/image334.gif)
.files/image336.gif) ,
,.files/image338.gif) 20
20
由.files/image340.gif) 及
及.files/image342.gif) 20与
20与.files/image141.gif) =3解得b=4,c=5或b=5,c= 4
=3解得b=4,c=5或b=5,c= 4
(3)设D到三边的距离分别为x、y、z,则.files/image344.gif)
.files/image346.gif) 又x、y满足
又x、y满足.files/image348.gif)
画出不等式表示的平面区域得:.files/image350.gif)
29(1)证明:连结.files/image352.gif) ,则
,则.files/image352.gif) //
//.files/image354.gif) ,
,
∵.files/image356.gif) 是正方形,∴
是正方形,∴.files/image358.gif) .∵
.∵.files/image360.gif) 面
面.files/image356.gif) ,∴
,∴.files/image363.gif) .
.
又.files/image365.gif) ,∴
,∴.files/image367.gif) 面
面.files/image369.gif) .
.
∵.files/image371.gif) 面
面.files/image369.gif) ,∴
,∴.files/image373.gif) ,
,
∴.files/image375.gif) .
.
.files/image376.gif) (2)证明:作
(2)证明:作.files/image378.gif) 的中点F,连结
的中点F,连结.files/image380.gif) .
.
∵.files/image382.gif) 是
是.files/image384.gif) 的中点,∴
的中点,∴.files/image386.gif)
.files/image388.jpg)
.files/image390.gif) ,
,
∴四边形.files/image392.gif) 是平行四边形,∴
是平行四边形,∴
.files/image394.gif) .
.
∵.files/image396.gif) 是
是.files/image384.gif) 的中点,∴
的中点,∴.files/image398.gif) ,
,
又.files/image400.gif) ,∴
,∴.files/image402.gif) .
.
∴四边形.files/image404.gif) 是平行四边形,
是平行四边形,.files/image406.gif) //
//.files/image408.gif) ,
,
∵.files/image410.gif) ,
,.files/image412.gif) ,
,
∴平面.files/image414.gif) 面
面.files/image220.gif) .
.
又.files/image417.gif) 平面
平面.files/image419.gif) ,∴
,∴.files/image218.gif) 面
面.files/image220.gif) .
.
(3).files/image422.gif) .
.
.files/image424.gif) .
.
30解:
(1)由.files/image224.gif) ,
,
得.files/image427.gif) ,
,
则由.files/image429.gif) ,解得F(3,0) 设椭圆
,解得F(3,0) 设椭圆.files/image228.gif) 的方程为
的方程为.files/image431.gif) ,
,
则.files/image433.gif) ,解得
,解得.files/image435.gif) 所以椭圆
所以椭圆.files/image228.gif) 的方程为
的方程为.files/image437.gif)
(2)因为点.files/image235.gif) 在椭圆
在椭圆.files/image228.gif) 上运动,所以
上运动,所以.files/image439.gif) , 从而圆心
, 从而圆心.files/image238.gif) 到直线
到直线.files/image233.gif) 的距离
的距离.files/image442.gif) . 所以直线
. 所以直线.files/image109.gif) 与圆
与圆.files/image238.gif) 恒相交
恒相交
又直线.files/image109.gif) 被圆
被圆.files/image238.gif) 截得的弦长为
截得的弦长为.files/image444.gif)
.files/image446.gif)
由于.files/image448.gif) ,所以
,所以.files/image450.gif) ,则
,则.files/image452.gif) ,
,
即直线.files/image109.gif) 被圆
被圆.files/image238.gif) 截得的弦长的取值范围是
截得的弦长的取值范围是.files/image452.gif)
31解:(1)g(t) 的值域为[0,.files/image454.gif) ]
]
(2).files/image456.gif)
(3)当.files/image458.gif) 时,
时,.files/image460.gif)
.files/image462.gif) ≤
≤.files/image464.gif) +
+.files/image466.gif) =
=.files/image468.gif) <2;
<2;
当.files/image470.gif) 时,
时,.files/image460.gif)
.files/image472.gif) ≤
≤.files/image474.gif) .
.
所以若按给定的函数模型预测,该市目前的大气环境综合指数不会超标。
32解:(1).files/image476.gif)
当.files/image478.gif) 时,
时,.files/image480.gif) 时,
时,.files/image482.gif) ,
,
.files/image484.gif)
.files/image486.gif) 的极小值是
的极小值是.files/image488.gif)
(2).files/image490.gif) ,
,.files/image492.gif) 要使直线
要使直线.files/image252.gif) 对任意的
对任意的.files/image254.gif) 都不是曲线
都不是曲线.files/image256.gif) 的切线,当且仅当
的切线,当且仅当.files/image495.gif) 时成立,
时成立,.files/image497.gif)
(3)因.files/image499.gif) 最大值
最大值
①当.files/image501.gif) 时,
时,.files/image503.gif)
.files/image505.gif)
②当.files/image507.gif) 时,
时,.files/image509.gif) (?)当
(?)当.files/image511.gif)
.files/image513.gif)
(?)当.files/image515.gif) 时,
时,.files/image517.gif) 在
在.files/image519.gif) 单调递增;
单调递增;
1°当.files/image521.gif) 时,
时,
.files/image523.gif)
.files/image525.gif) ;
;
2°当.files/image527.gif)
(?)当.files/image529.gif)
(?)当.files/image531.gif)
.files/image533.gif)
综上 .files/image535.gif)

 的展开式中,含x的项的系数是( )
的展开式中,含x的项的系数是( ) 的展开式中,含x的项的系数是( )
的展开式中,含x的项的系数是( )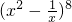 的展开式中,含x的项的系数是
的展开式中,含x的项的系数是![]() 的展开式中,含x的项的系数是
的展开式中,含x的项的系数是 ![]() 的展开式中,含x的项的系数是
的展开式中,含x的项的系数是