
题目列表(包括答案和解析)
如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(如图②)
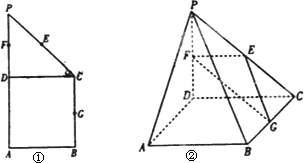
Ⅰ、求证AP∥平面EFG;
Ⅱ、求二面角G-EF-D的大小;
Ⅲ、在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证明.
如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将ΔPDC折起,使平面PDC⊥平面ABCD(如图②)

(1)求证AP∥平面EFG;
(2)求二面角G-EF-D的大小;
(3)在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证明.
(本题满分12分)
如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将ΔPDC折起,使平面PDC⊥平面ABCD(如图②)
(1)求证AP∥平面EFG;
(2)求二面角G-EF-D的大小;
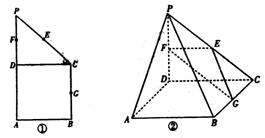 (3)在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证明。
(3)在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证明。
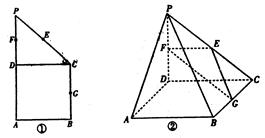
(本小题满分12)如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将ΔPDC折起,使PD⊥平面ABCD(如图②)
(1)求证AP∥平面EFG;
(2)求平面EFG与平面PDC所成角的大小;
(3)求点A到平面EFG的距离。

一、选择题:
1.C 2.D 3.C 4.A 5.B 6.C 7.B 8.A 9.D 10.A 11.A 12.C
二、填空题:
13..files/image250.gif) 14. 26 15. -3 16.
14. 26 15. -3 16. .files/image252.gif) 17. 3
18.
17. 3
18. .files/image254.gif)
19..files/image256.gif) 20.(0,1) 21.
20.(0,1) 21. .files/image258.gif) 22.
22..files/image260.gif) 23.765 24.5
23.765 24.5
25.2
26..files/image262.gif)
三、解答题:
27、解:(1)∵cos3x=4cos3x-3cosx,则.files/image193.gif) =4cos2x-3=2cos2x-1
=4cos2x-3=2cos2x-1
∴f(x)=2cos2x-1+2sin2x
=2.files/image265.gif) sin(2x+
sin(2x+.files/image242.gif) )-1
)-1
在2x+.files/image242.gif) =2kπ+
=2kπ+.files/image269.gif) 时,f(x)取得最大值2
时,f(x)取得最大值2.files/image265.gif) -1
-1
即在x=kπ+.files/image271.gif) (k∈Z)时,f(x)取得最大值2
(k∈Z)时,f(x)取得最大值2.files/image265.gif) -1
-1
(2)∵f(x)=2.files/image265.gif) sin(2x+
sin(2x+.files/image242.gif) )-1
)-1
要使f(x)递减,x满足2kπ+.files/image269.gif) ≤2x+
≤2x+.files/image242.gif) ≤2kπ+
≤2kπ+.files/image274.gif)
即kπ+.files/image271.gif) ≤x≤kπ+
≤x≤kπ+.files/image277.gif) (k∈Z)
(k∈Z)
又∵cosx≠0,即x≠kπ+.files/image269.gif) (k∈Z)
(k∈Z)
|