
题目列表(包括答案和解析)

| 2 |
| 3 |
| 3 |
| 5 |
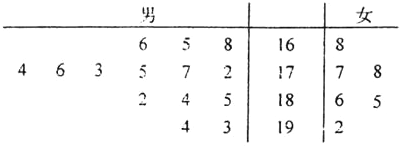 某公司由筛选出的男员工14名,女员工6名共20名员工组建甲、乙两个部门,现对这20名员工进行一次综合测试,成绩的茎叶图如下所示(单位:分).现规定l80分以上者到“甲部门”工作,1 80分以下者到“乙部门”工作.
某公司由筛选出的男员工14名,女员工6名共20名员工组建甲、乙两个部门,现对这20名员工进行一次综合测试,成绩的茎叶图如下所示(单位:分).现规定l80分以上者到“甲部门”工作,1 80分以下者到“乙部门”工作.| 2 | 3 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com