（本小题满分12分）[来源:学科网ZXXK]

某校高三文科分为四个班．高三数学调研测试后，

随机地在各班抽取部分学生进行测试成绩统计，

各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人。

抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示，

其中120～130(包括120分但不包括130分)的频率为0．05,此            0

分数段的人数为5人

（1）问各班被抽取的学生人数各为多少人?

（2）在抽取的所有学生中,任取一名学生, 求分数不小（本小题满分12分）

（本小题满分12分）

    某校一个甲类班x名学生在2011年某次数学测试中，成绩全部介于90分与140分之间，

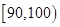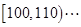将测试结果按如下方式分成五组，第一组；第二组第五组，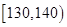

下表是按上述分组方法得到的频率分布表：

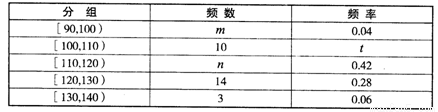
    （1）求x及分布表中m，n，t的值；

    （2）设a，b是从第一组或第五组中任意抽取的两名学生的数学测试成绩，求事件“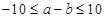的概率。”

（本小题满分12分）

某校高二文科分为四个班，期中测试后，随机地在各班抽取部分学生进行测试成绩统计，各班被抽取的学生人数恰好成等差数列，人数最少的班被抽取了22人，抽取出来的所有学生的测试成绩统计结果的频率分布的条形图如图所示，其中120-130（包括120分但不包括130分的频率为0.05，此分数段的人数为5人.

问各班被抽取的学生人数各为多少？

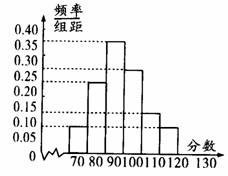在抽取的所有学生中，任取一名，求分数不少于90分的概率.

（本小题满分12分）

某校高二文科分为四个班，期中测试后，随机地在各班抽取部分学生进行测试成绩统计，各班被抽取的学生人数恰好成等差数列，人数最少的班被抽取了22人，抽取出来的所有学生的测试成绩统计结果的频率分布的条形图如图所示，其中120-130（包括120分但不包括130分的频率为0.05，此分数段的人数为5人.

问各班被抽取的学生人数各为多少？

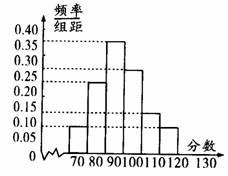在抽取的所有学生中，任取一名，求分数不少于90分的概率.

（本上题满分12分）某高校为了参加“CBA杯”安徽省大学生篮球联赛暨第十届CU—BA安徽省选拔赛，需要在各班选拔预备队员，规定投篮成绩甲级的可作为入围选手，选拔过程中每人投篮5次，若投中3次则确定为乙级，若投中4次及以上则可确定为甲级，一旦投中4次，即终止投篮，已知某班同学小明每次投篮投中的概率是0.6。（I）求小明投篮4次才被确定为乙级的概率；  （II）设小明投篮投中次数为X，求X的分布列及期望。