（1）利用单摆验证小球平抛运动规律，设计方案如图a所示，在悬点O正下方有水平放置的炽热的电热线P，当悬线摆至电热丝处时能轻易被烧断；MN为水平木板，已知悬线长为L，悬点到木板的距离OO′=h（h＞L）．

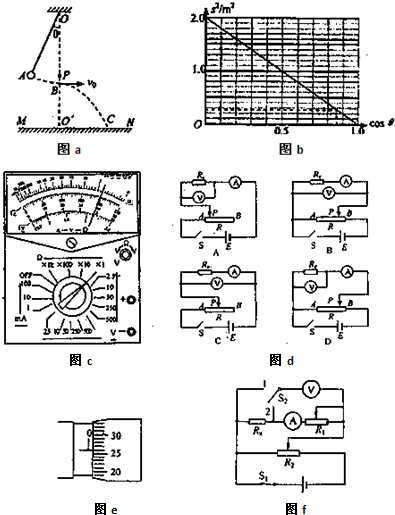
①将小球向左拉起后自由释放，最后小球落到木板上的C点，O′C=s，则小球做平抛运动的初速度为v₀=．
②在其他条件不变的情况下，若改变释放小球时悬线与竖直方向的夹角θ，小球落点与O'点的水平距离s将随之改变，经多次实验，以s²为纵坐标、cosθ为横坐标，得到如图b所示图象．则当θ=30°时，s为m；若悬线长L=1.0m，悬点到木板间的距离OO′为m．
（2）某学校实验室新进了一批低电阻的电磁螺线管．已知螺线管使用的金属丝电阻率ρ=1.7×10^-8Ω?m．课外活动小组的同学设计了一个试验来测算螺线管使用的金属丝长度．他们选择了多用电表、电流表、电压表、开关、滑动变阻器、螺旋测微器（千分尺）、导线和学生电源等．
①他们使用多用电表粗测金属丝的电阻，操作过程分以下三个步骤：（请填写第II步操作）
Ⅱ．；
Ⅲ．把红黑表笔分别与螺线管金属丝的两端相接，多用表的示数如图c所示．
②根据多用电表示数，为了减少实验误差，并在实验中获得较大的电压调节范围，应从图d的A、B、C、D四个电路中选择电路来测量金属丝电阻；
③他们使用千分尺测量金属丝的直径，示数如图e所示，金属丝的直径为mm；
④根据多用电表测得的金属丝电阻值，可估算出绕制这个螺线管所用金属丝的长度约为m．（结果保留两位有效数字）
⑤用电流表和电压表测量金属丝的电阻时，由于电压表、电流表内阻的影响，不论使用电流表内接法还是电流表外接法，都会产生系统误差．按如图f所示的电路进行测量，可以消除由于电表内阻造成的系统误差．利用该电路进行实验的主要操作步骤是：
第一步：先将R₂的滑动头调到最左端，单刀双掷开关S₂向1闭合，闭合开关S₁，调节滑动变阻器R₁和R₂，使电压表和电流表的示数尽量大些（在不超过量程的情况下），读出此时电压表和电流表的示数U₁、I₁．
第二步：保持两滑动变阻器滑动头位置不变，将单刀双掷开头S₂向2闭合，读出此时电压表和电流表的示数U₂、I₂．
请写出由以上记录数据计算被测电阻R_x的表达式R_x=．

利用如图甲所示的电路测定金属电阻率，在测量时需要用刻度尺测出被测金属丝的长度l，用螺旋测微器测出金属丝的直径d，用电流表和电压表测出金属丝的电阻R_x．

（1）请读出乙图中螺旋测微器的读数m
（2）写出测金属丝电阻率的表达式：ρ=．
（3）利用该电路进行实验的主要操作过程是：
第一步：闭合电键S₁，将电键S₂接2，调节滑动变阻器R_P和r，使电压表读数尽量接近满量程，读出这时电压表和电流表的示数U₁、I₁；
请你接着写出第二步，并说明需要记录的数据：．
由以上记录的数据计算出被测电阻R_x的表达式为R_x=．

（1）测量电阻的方法很多．某同学用伏安法测量B的电阻，已知电压表内阻约3千欧，电流表内阻约为1欧．若该同学用图甲电路，R_x的测量值比真实值（填“偏大”或“偏小”）；若被测电阻R_x的值约为10Ω，应采用图（选“甲”或“乙”）的电路，误差会比较小．
（2）无论是用图甲或图乙测量，都不可避免地产生由电表内阻引起的测量误差，有一个研究性学习小组设计了
以下的实验方案，用以避免电表内阻引起的系统误差．该方案是利用如图丙所示的电路进行测量，主要实验步骤如下：第一步：将开关S₂接2，闭合开关S₁，调节滑动变阻器R_p1和R_p2，
使电表读数接近满量程，但不超过量程，记录此时电压表和电流表的示数U₁、I₁．
①请你写出接着的第二步，并说明需要记录的数据：
②由以上记录的数据计算出被测电阻R_x的表达式R_x=．

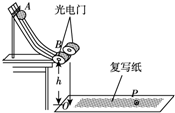某探究小组利用如图所示装置探究平抛运动中机械能是否守恒．在斜槽轨道的末端安装一个光电门B，调节激光束与球心等高，斜槽末端水平．地面上依次铺有白纸、复写纸，让小球从斜槽上固定位置A点无初速释放，通过光电门后落在地面的复写纸上，在白纸上留下打击印．重复实验多次，测得小球通过光电门的平均时间为2.50ms（毫秒）．当地重力加速度为9.8m/s²．
（1）小球直径为0.50cm，由此可知小球通过光电门的速度v_B=m/s；
（2）实验测得轨道离地面的高度h=0.441m，小球的平均落点P到轨道末端正下方O点的距离x=0.591m，则由平抛运动规律解得小球平抛的初速度v₀=m/s；
（3）在误差允许范围内，实验结果满足小球通过光电门的速度vB与由平抛运动规律求解的平抛初速度v₀满足关系，就可以认为平抛运动过程中机械能是守恒的．

2007年诺贝尔物理学奖授予了两位发现“巨磁电阻”效应的物理学家．材料的电阻随磁场的增加而增大的现象称为磁阻效应，利用这种效应可以测量磁感应强度．
若图1为某磁敏电阻在室温下的电阻-磁感应强度特性曲线，其中R_B、R₀分别表示有、无磁场时磁敏电阻的阻值．为了测量磁感应强度B，需先测量磁敏电阻处于磁场中的电阻值R_B．请按要求完成下列实验．
（1）设计一个可以测量磁场中该磁敏电阻阻值的电路图，在图2的虚线框内画出实验电路原理图（磁敏电阻及所处磁场已给出，待测磁场磁感应强度大小约为0.6～1.0T，不考虑磁场对电路其它部分的影响）．要求误差较小．提供的器材如下：
A．磁敏电阻，无磁场时阻值R₀=150Ω
B．滑动变阻器R，全电阻约20Ω
C．电流表A，量程2.5mA，内阻约30Ω
D．电压表V，量程3V，内阻约3KΩ
E．直流电源E，电动势3V，内阻不计
F．开关S，导线若干
（2）正确连线后，将磁敏电阻置于待测磁场中，测量数据如下表：

	1	2	3	4	5	6
U （V）	0.00	0.45	0.92	1.50	1.79	2.71
A （mA）	0.00	0.30	0.60	1.00	1.20	1.80

根据上表可求出磁敏电阻的测量值R_B=，结合图1可知待测磁场的磁感应强度B=T．
（3）试结合图1简要回答，磁感应强度B在0～0.2T和0.4～1.0T范围内磁敏电阻阻值的变化规律有何不同？
（4）某同学查阅相关资料时看到了图3所示的磁敏电阻在一定温度下的电阻-磁感应强度特性曲线（关于纵轴对称），由图线可以得到什么结论？