回旋加速器在核科学、核技术、核医学等高新技术领域得到了广泛应用，有力地推动了现代科学技术的发展。

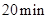 (1)当令医学影像诊断设备PET／CT堪称“现代医学高科技之冠”，它医疗诊断中，常利用能放射正电子的同位素碳11作示踪原子。碳11是由小型回旋加速器输出的高速质子轰击氮14获得，同时还产牛另一粒子，试写出核反应方程。若碳11的半衰期为,经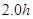剩余碳11的质量占原来的百分之几？（结果取两位有效数字）

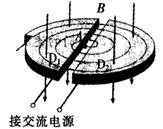
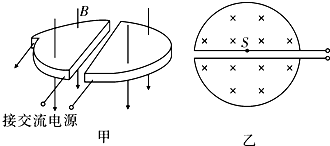
 (2)回旋加速器的原理如图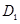．和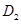是两个1中空半经为R的半圆金属盒，它们接在电压一定、频率为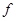的交流电源上，位于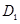圆心处的质子源A能不断产生质子(初速度可以忽略，重力不计)．它们在两盒之间被电场加速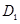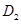，、置于与盒面垂直的磁感应强度为B的匀强磁场中。若质子束从回旋加速器输出时的平均功率为P．求输出时质子束的等效电流I与P、B、R、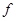的关系式(忽略质子在电场中的运动时间，其最大速度远小于光速)。

（3）推理说明：质子在回旋加速器中运动时，随轨道半径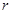的增大，同一盒中相邻轨道的半径之差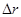是增大、减小还是不变？

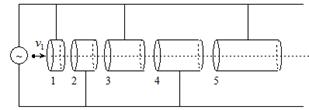
如图所示是一直线加速器原理的示意图，由Ｋ个长度逐个增大的共轴金属圆筒排列成一串（图中只画了5个作为示意），奇数筒和偶数筒分别连接到频率为f、最大电压值为Ｕ的正弦交流电源的两极（设圆筒内部没有电场），整个装置放在真空容器中，圆筒的两底面中心开有小孔。带电粒子从粒子源出发后，经过第一次加速，然后进入第一个圆筒，再向前运动。相邻两圆筒间的间隙很小，问：

　　 比荷为质子（），以沿轴线射入第一个圆筒，此时第1、2两个圆筒间的电势差为。（不计粒子的重力，不计粒子在两圆筒间运动的时间，不考虑相对论效应）

(1).要使质子每次在圆筒间都能获得最大的加速，质子穿越每个圆筒的时间最短为多大？

(2).在(1)的情形下，第n个圆筒的长度应为多大？若质子某次加速后动能为，则下一个圆筒长为多少？( )

(3).若利用回旋加速器使质子最终加速到动能为，则D形盒的半径应为多大？（D形盒中磁感应强度）