某空间存在水平方向的匀强电场(图中未画出)，带电小球沿如图8－3－20所示的直线斜向下由A点沿直线向B点运动，此空间同时存在由A指向B的匀强磁场，则下列说法正确的是                                                              (　　)．

A．小球一定带正电

B．小球可能做匀速直线运动

C．小球一定做匀加速直线运动

D．运动过程中，小球的机械能增大

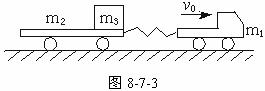
(1)当m₁、m₂、m₃以同一速度前进时，其速度的大小；

(2)物体在拖车平板上移动的距离(g取10 m/s²).

 (2013·苏北四市模拟)如图8－1－20所示，在竖直向下的匀强磁场中有两根竖直放置的平行粗糙导轨CD、EF，导轨上放有一金属棒MN.现从t＝0时刻起．给棒通以图示方向的电流且电流强度与时间成正比，即I＝kt，其中k为常量，金属棒与导轨始终垂直且接触良好．下列关于棒的速度v、加速度a随时间t变化的关系图象，可能正确的是                                                          (　　)．

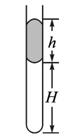
图8-5-3

在测定金属的电阻率的实验中，用该金属制成的长约(0.8m，直径小于1mm的电阻丝，电阻约5Ω左右。实验步骤如下：
(1)用米尺测量接入电路部分的金属导线的长度，测三次，求出平均值L。用叠绕法测出金属导线的直径d.
(2)用伏安法测量金属导线的电阻R．试把图8-4-3中所给出的器材连成测量R的合适线路，图中安培表的量程为0.6A，内阻接近1Ω，伏特表量程为3V，内阻为几kΩ，电源的电动势为6V，变阻器的阻值为0Ω～20Ω。要求在闭合电键前，变阻器的滑动触点应处于正确位置。
(3)用上面测得的L、d和R，根据电阻率的表达式ρ=______，算出所测金属的电阻率。