（2013•绥化）已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上一动点（点D不与点B，C重合）．以AD为边做正方形ADEF，连接CF
（1）如图1，当点D在线段BC上时．求证CF+CD=BC；
（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF，BC，CD三条线段之间的关系；
（3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线BC的两侧，其他条件不变；
①请直接写出CF，BC，CD三条线段之间的关系；
②若正方形ADEF的边长为2

2

，对角线AE，DF相交于点O，连接OC．求OC的长度．

（2013•东营）（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．
证明：DE=BD+CE．
（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．

（2013•温州模拟）选择用反证法证明“已知：在△ABC中，∠C=90°．求证：∠A，∠B中至少有一个角不大于45°．”时，应先假设（　　）

（2013•门头沟区一模）已知：在△ABC中，AB=AC，点D为BC边的中点，点F是AB边上一点，点E在线段DF的延长线上，点M在线段DF上，且∠BAE=∠BDF，∠ABE=∠DBM．

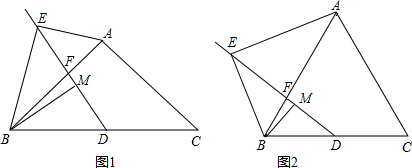
（1）如图1，当∠ABC=45°时，线段DM与AE之间的数量关系是；
（2）如图2，当∠ABC=60°时，线段DM与AE之间的数量关系是；
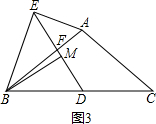
（3）①如图3，当∠ABC=α（0°＜α＜90°）时，线段DM与AE之间的数量关系是；
②在（2）的条件下延长BM到P，使MP=BM，连结CP，若AB=7，AE=2

7

，求sin∠ACP的值．