（本题10分）某服装厂现有A种布料70m，B种布料52m，现计划用这两种布料生产M, N两种型号的时装80套，已知做一套M型号的时装需要A种布料0.6m，B种布料0.9m，可获利45元，做一套N型号的时装需要A种布料1.1m，B种布料0.4m，可获利50元，若设生产N型号的时装套数为x，用这批布料生产这两种型号的时装所获的总利润为y元。
【小题1】（1）求y与x的函数关系式，并求出自变量x的取值范围。
【小题2】（2）该服装厂在生产这批时装中，当生产N型号的时装多少套时，所获利润最大？最大利润是多少？

（本题10分）如图，矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上，且OD＝10，OB＝8．将矩形的边BC绕点B逆时针旋转，使点C恰好与x轴上的点A重合．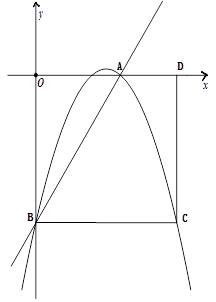

(1)直接写出点A、B的坐标：A(    ，     )、B(     ，     )；
(2)若抛物线y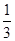＝－x²＋bx＋c经过点A、B，请求出这条抛物线的解析式；
(3)当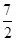≤x≤7，在抛物线上存在点P，使△ABP的面积最大，那么△ABP最大面积是                                 ．（请直接写出结论，不需要写过程）

（本题10分） 随着大陆惠及台胞政策措施的落实，台湾水果进入了大陆市场。一水果经销商购进了A，B两种台湾水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售。预计每箱水果的盈利情况如下表：

  有两种配货方案（整箱配货）：

方案一：甲、乙两店各配货10箱，其中A种水果两店各5箱，B种水果两店各5箱；

方案二：按照甲、乙两店盈利相同配货，其中A种水果甲店_________箱，乙店__________箱；B种水果甲店_________箱，乙店__________箱.

（1）   如果按照方案一配货，请你计算出经销商能盈利多少元？

（2）   请你将方案二填写完整（只填写一种情况即可），并根据你填写的方案二与方案一作比较，哪种方案盈利较多？

（3）   在甲、乙两店各配货10箱，且保证乙店盈利不小于100元的条件下，请你设计出使水果经销商盈利最大的配货方案，并求出最大盈利为多少？

（本题10分）食品厂生产的一种巧克力糖每千克成本为24元，其销售方案有如下两种：

方案1若直接给本厂设在某地的门市部销售，则每千克售价为32元，但门市部每月需要有关费用2400元。

方案2若直接批发给超市销售，则出厂价为每千克28元。

若每月只能按一种方案销售，且每种方案都能按月销售完当月产品，设该厂每月的销售量为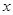千克。

1.（1）如果你是厂长，应该如何选择销售方案，可使工厂当月所获利润更大？

2.（2）厂长看到会计送来的第一季度销售量与利润关系的报表（如下表）后，发现该表填写的销售量与实际有不符之处，请找出不符之处，并计算第一季度的实际销售总量

(本题10分)为了解八年级学生的课外阅读情况，我校语文组从八年级随机抽取了若干名学生，对他们的读书时间进行了调查并将收集的数据绘成了两幅不完整的统计图，请你依据图中提供的信息，解答下列问题：（每组含最小值不含最大值）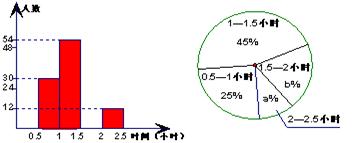
 
【小题1】⑴从八年级抽取了多少名学生？
【小题2】⑵填空(直接把答案填到横线上)
①“2—2.5小时”的部分对应的扇形圆心角为_______度；
②课外阅读时间的中位数落在________(填时间段)内．
【小题3】⑶如果八年级共有800名学生，请估算八年级学生课外阅读时间
不少于1.5小时的有多少人？