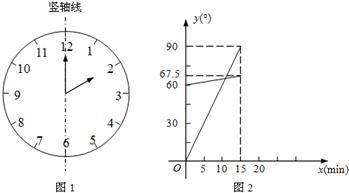
（8分）（1）在遇到问题：“钟面上，如果把时针与分针看作是同一平面内的两条线段，在2∶00~2∶15之间，时针与分针重合的时刻是多少？”时，小明尝试运用建立函数关系的方法：

①恰当选取变量x和y．小明设2点钟之后经过x min（0≤x≤15），时针、分针分别与竖轴线（即经过表示“12”和“6”的点的直线，如图1）所成的角的度数为y₁°、y₂°；

②确定函数关系．由于时针、分针在单位时间内转动的角度不变，因此既可以直接写出y₁、y₂关于x的函数关系式，也可以画出它们的图象．小明选择了后者，画出了图2；

③根据题目的要求，利用函数求解．本题中小明认为求出两个图象交点的横坐标就可以解决问题．

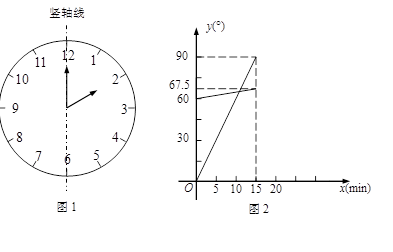
请你按照小明的思路解决这个问题．

（2）请运用建立函数关系的方法解决问题：钟面上，如果把时针与分针看作是同一平面内

的两条线段，在7∶30~8∶00之间，时针与分针互相垂直的时刻是多少？

（本题12分）在梯形ABCD中，AB∥CD,∠BCD=90,且AB=1,BC=2，tan∠ADC=2;对角线相交于O点，等腰直角三角板的直角顶点落在梯形的顶点C上，使三角板绕点C旋转。

（1）当三角板旋转到图1的位置时，猜想DE与BF的数量关系，并加以证明。

（2）在（1）问条件下，若BE：CE=1：2，∠BEC=135°,求sin∠BFE的值。

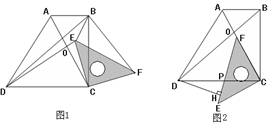（3）当三角板的一边CF与梯形对角线AC重合时，作DH⊥PE于H,如图2，若OF=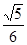时，求PE及DH的长。

（本题8分）如图，在梯形ABCD中，AD//BC，E是AD的中点，BC=5，AD=12，梯形高为4，∠A =45°，P为AD边上的动点.

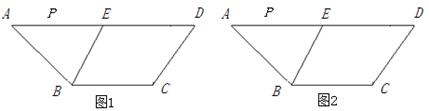
（1）当PA的值为____________时，以点P、B、C、E为顶点的四边形为直角梯形；

（2）当PA的值为____________时，以点P、B、C、E为顶点的四边形为平行四边形；

（3）点P在AD边上运动的过程中，以P、B、C、E为顶点的四边形能否构成菱形？如果能，求出PA长．如果不能，也请说明理由.

（本题8分）如图，在梯形ABCD中，AD//BC，E是AD的中点，BC=5，AD=12，梯形高为4，∠A =45°，P为AD边上的动点.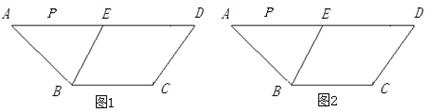

（1）当PA的值为____________时，以点P、B、C、E为顶点的四边形为直角梯形；
（2）当PA的值为____________时，以点P、B、C、E为顶点的四边形为平行四边形；
（3）点P在AD边上运动的过程中，以P、B、C、E为顶点的四边形能否构成菱形？如果能，求出PA长．如果不能，也请说明理由.