
题目列表(包括答案和解析)
已知函数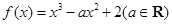 ,
,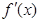 为
为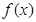 的导函数。 (1)求函数
的导函数。 (1)求函数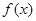 的单调递减区间;
的单调递减区间;
(2)若对一切的实数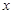 ,有
,有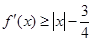 成立,求
成立,求 的取值范围;
的取值范围;
(3)当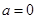 时,在曲线
时,在曲线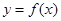 上是否存在两点
上是否存在两点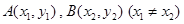 ,使得曲线在
,使得曲线在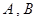 两点处的切线均与直线
两点处的切线均与直线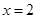 交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.
交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.
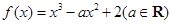 ,
,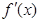 为
为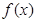 的导函数。 (1)求函数
的导函数。 (1)求函数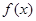 的单调递减区间;
的单调递减区间;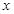 ,有
,有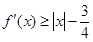 成立,求
成立,求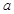 的取值范围;
的取值范围; 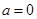 时,在曲线
时,在曲线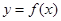 上是否存在两点
上是否存在两点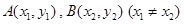 ,使得曲线在
,使得曲线在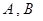 两点处的切线均与直线
两点处的切线均与直线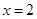 交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.
交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.已知函数 ,(
,(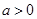 ),
),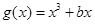
(1)若曲线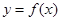 与曲线
与曲线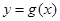 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当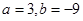 时,若函数
时,若函数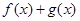 在区间[k,2]上的最大值为28,求k的取值范围
在区间[k,2]上的最大值为28,求k的取值范围
【解析】(1)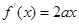 ,
,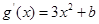
∵曲线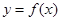 与曲线
与曲线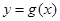 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴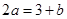 ,
,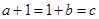
∴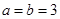
(2)当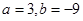 时,
时,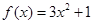 ,
,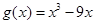 ,
,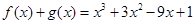
令 ,则
,则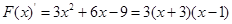 ,令
,令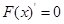 ,
, ∴
∴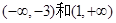 为单调递增区间,
为单调递增区间,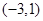 为单调递减区间,其中F(-3)=28为极大值,所以如果区间[k,2]最大值为28,即区间包含极大值点
为单调递减区间,其中F(-3)=28为极大值,所以如果区间[k,2]最大值为28,即区间包含极大值点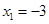 ,所以
,所以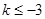
【考点定位】此题应该说是导数题目中较为常规的类型题目,考查的切线,单调性,极值以及最值问题都是课本中要求的重点内容,也是学生掌握比较好的知识点,在题目中能够发现F(-3)=28,和分析出区间[k,2]包含极大值点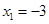 ,比较重要
,比较重要
| 4+2b-b2 |
| 1-(x-a)2 |
| θ |
| 2 |
| π |
| 2 |
A;A;C;D;A;A; C;C;B;C(文)D(理);C;A
13、 或
或 ; 14、80; 15、(理)
; 14、80; 15、(理) (文)-2; 16、
(文)-2; 16、 ;
;
17、解:⑴
 ………………………………………3分
………………………………………3分
 时,由
时,由 得函数的递增区间为
得函数的递增区间为
 时,由
时,由 得函数的递增区间为
得函数的递增区间为
…………………………………………………………………………………………………………………5分
⑵
 …………………………………………………………7分
…………………………………………………………7分
 时,
时, 得:
得: (舍)
(舍)
 时,
时, 得
得
综上, ………………………………………………………………………………10分
………………………………………………………………………………10分
18、解:用 分别表示三列火车正点到达的事件,则
分别表示三列火车正点到达的事件,则

⑴恰有两列火车正点到达的概率记为 ,则
,则
 ……………………………………………6分
……………………………………………6分
⑵(文科)用 表示误点的列数,则至少两列误点可表示为:
表示误点的列数,则至少两列误点可表示为:

 ……………………………………………………………………………………12分
……………………………………………………………………………………12分
(理科)三列火车正点的列数分别为 。则
。则



 ……………………………………………………………10分
……………………………………………………………10分
 …………………………12分
…………………………12分
19.解:方法一:(I)证明:,
又 平面平面ABCD,平面平面ABCD=BC,
平面平面ABCD,平面平面ABCD=BC,

平面ABCD ……2分
在梯形ABCD中,可得
,即
在平面ABCD内的射影为AO, ……4分
(II)解:,且平面平面ABCD
平面PBC, 平面PBC,
为二面角P―DC―B的平面角 ……6分
是等边三角形即二面角P―DC―B的大小为 …8分
(III)证明:取PB的中点N,连结CN, ①
①
,且平面平面ABCD,平面PBC ……10分
平面PAB 平面平面PAB ②
由①、②知平面PAB…………..10分
连结DM、MN,则由MN//AB//CD, ,
,
得四边形MNCD为平行四边形,,平面PAB.
平面PAD 平面平面PAB ……………….12分
方法二:取BC的中点O,因为是等边三角形,
由侧面底面ABCD 得底面ABCD ……1分
以BC中点O为原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,建立如图所示的空间直角坐标系O―xyz……2分

(I)证明:,则在直角梯形中,
在等边三角形PBC中,……3分


 ,即…4分
,即…4分
(II)解:取PC中点N,则

平面PDC,显然,且平面ABCD
所夹角等于所求二面角的平面角 ……6分

 ,二面角的大小为 ……8分
,二面角的大小为 ……8分
(III)证明:取PA的中点M,连结DM,则M的坐标为
又 ……10分
……10分
 ,
,
 即
即
平面PAB,平面平面PAB ……12分
20.解:Ⅰ由已知得: …………………………………………………………2分
…………………………………………………………2分
当 解得:
解得: ……………………………………………………3分
……………………………………………………3分
当 时,
时, ,带入上式得:
,带入上式得:
配方得:
所以 ……………………………………………………………5分
……………………………………………………………5分
所以 ………………………………………………7分
………………………………………………7分
Ⅱ(文科)
 ……………………………………………………………………………………10分
……………………………………………………………………………………10分
 …………………………………12分
…………………………………12分
(理科)
 ………………………………………………………………………………9分
………………………………………………………………………………9分
 ……………………11分
……………………11分
 …………………………………………………………12分
…………………………………………………………12分
22.解:⑴ ;
;
当 时,
时, ;
;
令 ,该二次函数的对称轴为
,该二次函数的对称轴为
当 时,设
时,设 ,
, ,则
,则 ;
;
当 时,要使
时,要使 在
在 上是单调函数,只能为
上是单调函数,只能为 上的减函数
上的减函数
故函数 在
在 上满足:
上满足:
 或
或 ,解得
,解得 。综上
。综上 ………4分
………4分
⑵当 时,
时, ;
;
当 ;当
;当

所以 …………………………………………………4分
…………………………………………………4分
⑶反证法:不妨设 ,由⑵知
,由⑵知
所以
所以


所以 ;
;
因为 时,
时, 这与上面的结论矛盾,故
这与上面的结论矛盾,故
同理 ……………………………………………12分
……………………………………………12分
(文)解:⑴
则 ,所以
,所以 ……………………………3分
……………………………3分
 ;由此可知
;由此可知
当 时,函数
时,函数 单调递增
单调递增
当 时,函数
时,函数 单调递减,
单调递减,
当 时,函数取极大值
时,函数取极大值 ………………………………………………………………6分
………………………………………………………………6分
⑵ 在区间
在区间 上是单调减函数,
上是单调减函数,
所以 在区间
在区间 上恒成立,由二次函数的图像可知:
上恒成立,由二次函数的图像可知:
 ;令
;令 …………………………………………………9分
…………………………………………………9分
当直线 经过交点
经过交点 时,取得最小值
时,取得最小值 …………………………………12分
…………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com