
题目列表(包括答案和解析)
已知数列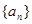 满足
满足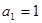 ,
,
(1)求证:数列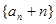 是等比数列;
是等比数列;
(2)求数列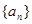 的通项和前n项和
的通项和前n项和 .
.
【解析】第一问中,利用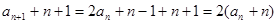 ,得到
,得到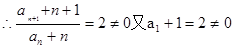 从而得证
从而得证
第二问中,利用∴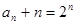 ∴
∴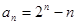 分组求和法得到结论。
分组求和法得到结论。
解:(1)由题得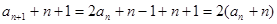 ………4分
………4分
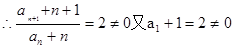 ……………………5分
……………………5分
∴数列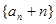 是以2为公比,2为首项的等比数列;
……………………6分
是以2为公比,2为首项的等比数列;
……………………6分
(2)∴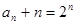 ……………………8分
……………………8分
∴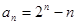 ……………………9分
……………………9分
∴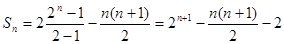
如图,三棱柱 中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。
中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。

(I) 证明:平面 ⊥平面
⊥平面
(Ⅱ)平面 分此棱柱为两部分,求这两部分体积的比.
分此棱柱为两部分,求这两部分体积的比.
【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计算,考查空间想象能力、逻辑推理能力,是简单题.
【解析】(Ⅰ)由题设知BC⊥ ,BC⊥AC,
,BC⊥AC, ,∴
,∴ 面
面 , 又∵
, 又∵
 面
面 ,∴
,∴ ,
,
由题设知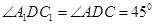 ,∴
,∴ =
= ,即
,即 ,
,
又∵ , ∴
, ∴ ⊥面
⊥面 , ∵
, ∵
 面
面 ,
,
∴面 ⊥面
⊥面 ;
;
(Ⅱ)设棱锥 的体积为
的体积为 ,
, =1,由题意得,
=1,由题意得, =
= =
= ,
,
由三棱柱 的体积
的体积 =1,
=1,
∴ =1:1, ∴平面
=1:1, ∴平面 分此棱柱为两部分体积之比为1:1
分此棱柱为两部分体积之比为1:1
(理)(本小题8分)如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形,
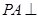 平面
平面 ,
,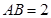 ,
, ,以
,以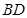 的中点
的中点 为球心、
为球心、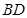 为直径的球面交
为直径的球面交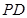 于点
于点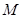 .
.
(1) 求证:平面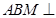 平面
平面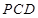 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
证明:(1)由题意,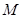 在以
在以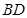 为直径的球面上,则
为直径的球面上,则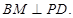
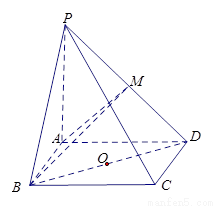
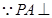 平面
平面 ,则
,则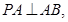
又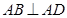 ,
,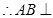 平面
平面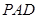 ,
,
∴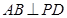 ,
,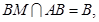
 平面
平面 ,
,
∴平面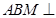 平面
平面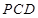 . (3分)
. (3分)
(2)∵ 是
是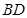 的中点,则
的中点,则 点到平面
点到平面 的距离等于点
的距离等于点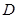 到平面
到平面 的距离的一半,由(1)知,
的距离的一半,由(1)知,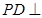 平面
平面 于
于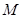 ,则线段
,则线段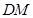 的长就是点
的长就是点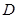 到平面
到平面 的距离
的距离

∵在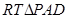 中,
中,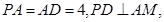
∴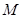 为
为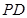 的中点,
的中点,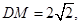 (7分)
(7分)
则点 到平面
到平面 的距离为
的距离为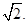 (8分)
(8分)
(其它方法可参照上述评分标准给分)
某市投资甲、乙两个工厂,2011年两工厂的产量均为100万吨,在今后的若干年内,甲工厂的年产量每年比上一年增加10万吨,乙工厂第 年比上一年增加
年比上一年增加 万吨,记2011年为第一年,甲、乙两工厂第
万吨,记2011年为第一年,甲、乙两工厂第 年的年产量分别为
年的年产量分别为 万吨和
万吨和 万吨.
万吨.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)若某工厂年产量超过另一工厂年产量的2倍,则将另一工厂兼并,问到哪一年底,其中哪一个工厂被另一个工厂兼并.
【解析】本试题主要考查数列的通项公式的运用。
第一问由题得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98
第二问,考查等差数列与等比数列的综合,考查用数列解决实际问题,其步骤是建立数列模型,进行计算得出结果,再反馈到实际中去解决问题.由于比较两个工厂的产量时两个函数的形式较特殊,不易求解,故采取了列举法,数据列举时作表格比较简捷.
解:(Ⅰ)由题得an=10n+90,bn=100+2+22+23+…+2n-1=100+2(1-2n-1)/ 1-2 =2n+98……6分
(Ⅱ)由于n,各年的产量如下表
n 1 2 3 4 5 6 7 8
an 100 110 120 130 140 150 160 170
bn 100 102 106 114 130 162 226 354
2015年底甲工厂将被乙工厂兼并
已知正数数列{an }中,a1 =2.若关于x的方程 (
( )对任意自然数n都有相等的实根.
)对任意自然数n都有相等的实根.
(1)求a2 ,a3的值;
(2)求证
【解析】(1)中由题意得△ ,即
,即 ,进而可得
,进而可得 ,.
,.
(2)中由于 ,所以
,所以 ,因为
,因为 ,所以数列
,所以数列 是以
是以 为首项,公比为2的等比数列,知数列
为首项,公比为2的等比数列,知数列 是以
是以 为首项,公比为
为首项,公比为 的等比数列,利用裂项求和得到不等式的证明。
的等比数列,利用裂项求和得到不等式的证明。
(1)由题意得△ ,即
,即 ,进而可得
,进而可得
(2)由于 ,所以
,所以 ,因为
,因为 ,所以数列
,所以数列 是以
是以 为首项,公比为2的等比数列,知数列
为首项,公比为2的等比数列,知数列 是以
是以 为首项,公比为
为首项,公比为 的等比数列,于是
的等比数列,于是
 ,
,
所以
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com