阅读下面材料,并解答下列各题:
在形如a
b=N的式子中,我们已经研究过两种情况:
①已知a和b,求N,这是乘方运算;
②已知b和N,求a,这是开方运算;
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算.
定义:如果a
b=N(a>0,a≠1,N>0),则b叫做以a为底N的对数,记着b=log
aN.
例如:因为2
3=8,所以log
28=3;因为
2-3=,所以
log2=-3.
(1)根据定义计算:
①log
381=
;②log
33=
;③log
31=
;
④如果log
x16=4,那么x=
.
(2)设a
x=M,a
y=N,则log
aM=x,log
aN=y(a>0,a≠1,M、N均为正数),
∵a
x•a
y=a
x+y,∴a
x+y=M•N∴log
aMN=x+y,
即log
aMN=log
aM+log
aN
这是对数运算的重要性质之一,进一步,我们还可以得出:
log
aM
1M
2M
3…M
n=
(其中M
1、M
2、M
3、…、M
n均为正数,a>0,a≠1)
log
a=
(a>0,a≠1,M、N均为正数).

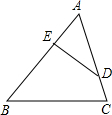 解答下列各题
解答下列各题 解答下列各题
解答下列各题 并把解集表示在数轴上.
并把解集表示在数轴上.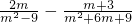
 )2+
)2+ =0,求xy-
=0,求xy- 的值.
的值.