练习册

  • 练习册
  • 试题
    当时.点为原点.为轴.为轴.点也为原点.从而点也为原点.因此点的轨迹的方程为.它表示以原点为顶点.以为焦点的抛物线, 【查看更多】

     

    题目列表(包括答案和解析)

    以O为原点，
    OF
    所在直线为x轴，建立直角坐标系．设
    OF
    •
    FG
    =1    ，点F的坐标为（t，0），t∈[3，+∞）．点G的坐标为（x0，y0）．
    （1）求x0关于t的函数x0=f（t）的表达式，并判断函数f（x）的单调性．
    （2）设△OFG的面积S=
    		31
    6
    t    ，若O以为中心，F，为焦点的椭圆经过点G，求当|
    OG
    |    取最小值时椭圆的方程．
    （3）在（2）的条件下，若点P的坐标为(0，
    9
    2
    )    ，C，D是椭圆上的两点，
    PC
    =λ
    PD
    (λ≠1)    ，求实数λ的取值范围．

    查看答案和解析>>

    以O为原点，
    OF
    所在直线为x轴，建立直角坐标系．设
    OF
    •
    FG
    =1    ，点F的坐标为（t，0），t∈[3，+∞）．点G的坐标为（x0，y0）．
    （1）求x0关于t的函数x0=f（t）的表达式，并判断函数f（x）的单调性．
    （2）设△OFG的面积S=
    		31
    6
    t    ，若O以为中心，F，为焦点的椭圆经过点G，求当|
    OG
    |    取最小值时椭圆的方程．
    （3）在（2）的条件下，若点P的坐标为(0，
    9
    2
    )    ，C，D是椭圆上的两点，
    PC
    =λ
    PD
    (λ≠1)    ，求实数λ的取值范围．

    查看答案和解析>>

    质点由原点出发时开始计时，沿x轴运动，其加速度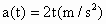，当初速度v(0)=0时，质点出发后6s所走的路程为

    [　　]

    A．36

    B．54

    C．72

    D．96

    查看答案和解析>>

    当极点在原点，极轴为x轴的正半轴，且取相同的长度单位时，直线ι1的参数方程为(t为参数)．直线ι2极坐标方程为．则直线ι1与ι2的夹角是

    ［　　 ］

    查看答案和解析>>

    如图，点An(xn，yn)是曲线y2＝2x(y≥0)上的点，点Bn(an，0)是x轴上的点，△Bn－1AnBn是以An为直角顶点的等腰直角三角形，其中n＝1，2，3，…，B0为坐标原点．

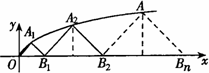
    (Ⅰ)求数列{an}的通项公式；

    (Ⅱ)设数列bn＝2n－1，求最小正整数m，使得对任意的n∈N*，当n＞m时，an＜bn成立．

    查看答案和解析>>


    同步练习册答案