题目列表(包括答案和解析)
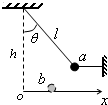
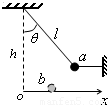
一根长度为L的绝缘细线上端固定下端系一质量为m的带正电小球，将它放置在一水平向右的匀强电场中，已知细线向右偏到和竖直线成
角时，小球处于平衡状态。现在将小球拉到与竖直线成某一角度
由静止释放，当小球运动到竖直位置时速度恰好为零。
求：
（1）角度的大小？
（2）小球在运动过程中，细线的最大拉力为多少？（已知
，
，重力加速度为g）（本小题8分）
如下图所示，绝缘细线长为l，一端固定在O点，另一端系一个质量为m，带电荷量为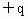
的小球，整个装置处于垂直于纸面向里的磁感应强度为B的匀强磁场中，将小球从细线跟竖直方向的夹角为θ的A点无初速释放，小球摆动过程中的最低点为B，则
[ ]
A．小球向右和向左运动通过B点时小球的速度相同
B．小球向右和向左运动通过B点时小球的加速度相同
C．小球向右和向左运动通过B点时具有相同的动能
D．小球向右和向左运动通过B点时受到细线的拉力相同
一．(20分)填空题．
1．或门 非门
2．静摩擦力 
v
3． 升高 hL/(H-h)
4．Ba2 2n2B
5． 一直变小 
二．（40分）选择题．
第Ⅰ部分（单选）
6．C
7．D
8．D
9．B
10．D
第Ⅱ部分（多选）
11．B D
12．A C
13．B C
14．B C D
三．(30分)实验题．
15．（1）乙 （2）图略 （3）A C D
16．BCADE 或BCDAE ，
用手拉其中一条细绳套，弹簧秤拉另一条细绳套，记下O点、弹簧秤读数F1和两条细绳套的方向，然后互换手拉和弹簧秤拉细绳套，产生同样效果，可读出F2，其他步骤相同。
17．（1）C （2）缩小 （3）光波的波长成正比 长
18．（1）否（1分） （2）偏低（1分） （3）271．3. K～325 .6K
（或-
19．（1）在连续相等时间内的位移 （2） 图略 （3） 倾角过大，未平衡摩擦力 （4）变大
四、（60分）计算题（本大题共5道题）
20（10分）（1） 气体等压变化 
（3分）
气缸移动的距离为 
(1分)
（2）
从状态1→3气体等容变化 
（3分）
P3 S= P0 S+ F F = (P3－P0 )S = 1×104×10-2N = 100N （3分）
21．
解：某同学对飞机作匀速直线运动的分析正确 （2分）
但对飞机作匀加速直线运动分析错误
分析： ①飞机经观察点正上方时有水平初速度，而该同学没有意识到初速度的因素，运用了初速为零的规律。②L1是炸弹的水平位移而不是飞机的水平位移，该同学将其混淆了。 （2分）
解答：
设飞机第一次投弹时的速度为v1，第二次投弹时的速度为v2，则有L1=v1t，（1分） v2=v1+a t，（1分） L2－
= v2t ， （2分） 联立以上三式，
解得飞机的加速度为
（2分）
22．解：（1）根据闭合电路欧姆定律
（2分）
（1分）
联立方程求得 Rx = (U2－U1)R1/U1 （2分）
（或说明将S2切换到a或切换到b， 电流不变，故
解出Rx同样给分）
（2）利用图线的截距求E
（2分）
令
即得E = U = 2v （2分）
将数据
、
、 E = 2v 代入上式得 r = 0.5Ω （3分）
（通过图线斜率1/I求解r同样给分）
23．（1） F1S1 =ηE0 （3分）
（1分）
（2）
（1分）
（1分）
（1分） （1分）
（3）
（1分）
（1分）
（1分）
 |
（2分）
（1分）
24．（1）在时刻t，有
（1分）
（1分）
（1分）
所以在t时刻金属杆MN产生的感应电动势大小为
（1分）
（2）在t时刻金属杆MN所受的安培力大小为
（2分）
F－F安=
m a 外力F
= F安+ m
a = 
+ ma （1分）
（3）位移为x时，此过程中磁感应强度的平均值
=
（1分）
回路面积△S = x l （1分）
感应电动势的平均值
（2分）
（4）撤去拉力F，金属杆MN作加速度不断变化的减速运动（变减速运动）（1分）
此后电路发出的热量为 Q = 
（2分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com