天星
13. ; 14.-10,2; 15.
; 14.-10,2; 15. ; 16.540
; 16.540
三、简答题
17.(1) ,
,
cosC= ,C=
,C=
(2)c2=a2+b2-2abcosC,c= ,
, =a2+b2-ab=(a+b)2-3ab.
=a2+b2-ab=(a+b)2-3ab.
S= abs1nC=
abs1nC= abs1n
abs1n =
= ab=
ab=
Ab=6,(a+b)2= +3ab=
+3ab= +18=
+18= ,a+b=
,a+b=
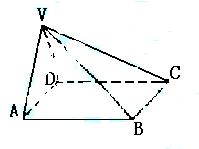
18.方法一:(1)解:取AD中点O,连结PO,BO.
△PAD是正三角形,所以PO⊥AD,…………1分
又因为平面PAD⊥平面ABCD,所以,PO⊥平面ABCD, …………3分
BO为PB在平面ABCD上的射影,
所以∠PBO为PB与平面ABCD所成的角.…………4分
由已知△ABD为等边三角形,所以PO=BO= ,
,
所以PB与平面ABCD所成的角为45° ………5分
(2)△ABD是正三角形,所以AD⊥BO,所以AD⊥PB, ………………6分
又,PA=AB=2,N为PB中点,所以AN⊥PB, ………………8分
所以PB⊥平面ADMN. ………………9分
(3)连结ON,因为PB⊥平面ADMN,所以ON为PO在平面ADMN上的射影,
因为AD⊥PO,所以AD⊥NO, ………………11分
故∠PON为所求二面角的平面角. ………………12分
因为△POB为等腰直角三角形,N为斜边中点,所以∠PON=45°,
19.(1) 随意抽取4件产品检查是随机事件,而第一天有9件正品
随意抽取4件产品检查是随机事件,而第一天有9件正品
 第一天通过检查的概率为
第一天通过检查的概率为 ……5分
……5分
(2)同(1),第二天通过检查的概率为 ……7分
……7分
因第一天,第二天是否通过检查相互独立
所以,两天全部通过检查的概率为: ……10分
……10分
(3)记得分为 ,则
,则 的值分别为0,1,2
的值分别为0,1,2
 ……11分
……11分
 ……12分
……12分
 ……13分
……13分
因此,
20.(1)yn=2logaxn,yn+1=2logaxn+1 ,yn+1 ? yn=2[logaxn+1
? logaxn]=2loga
{xn}为等比数, 为定值,所以{yn}为等差数列
为定值,所以{yn}为等差数列
又因为y6- y3=3d=-6,d=-2,y1=y3-2d =22,
Sn=22n+ = - n2+23n,故当n=11或n=12时,Sn取得最大值132
= - n2+23n,故当n=11或n=12时,Sn取得最大值132
(2)yn=22+(n-1)(-2)=2logaxn,xn=a12-n>1
当a>1时,12-n>0, n<12;当0<a<1时,12-n<0 n>12,
所以当0<a<1时,存在M=12,当n>M时,xn>1恒成立。
21.(1)设点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,
,
由 ,解得
,解得 ,所以
,所以

 .
.
当且仅当 时,
时, 取到最大值
取到最大值 .
.
(2)由 得
得 ,
,
 ,
,

 . ②
. ②
设 到
到 的距离为
的距离为 ,则
,则 ,又因为
,又因为 ,
,
所以 ,代入②式并整理,得
,代入②式并整理,得 ,
,
解得 ,
, ,代入①式检验,
,代入①式检验, ,
,
故直线 的方程是
的方程是
 或
或 或
或 ,或
,或 .
.
22.(1)由K=e得f(x)=ex-ex, 所以f’(x)=ex-e. 由f’(x)>0得x>1,故f(x)的单调增区间
为(1,+∞),由f’(x)<0得x<1,故f(x)的单调递减区间为(-∞,1)(3分)
(2)由f(|x|)>0对任意x∈R成立等价于f(x)>0对任意x≥0成立。由f’(x)=ex-k=0得x=lnk.
①当k∈(0,1) 时 ,f’(x)=ex-k ≥1-k≥0(x>0),此时f(x)在(0,+∞上单调递增,故f(x)
≥f(0)==1>),符合题意。②当k∈(1,+∞)时,lnk>0,当X变化时,f’(x)、f(x)的变化情况
如下表:
X
(0,lnk)
lnk
(lnk,+ ∞)
f’(x)
-
0
+
f(x)
单调递减
极小值
单调递增

由此可得,在(0,+∞)上f(x)≥f(lnk)=k-lnk.依题意,k-klnk>0,又k>1,所以1<k<e.
综上所述,实数k的取值范围是0<k<e. (8分)
(3)因为F(x)=f(x)+f(-x)=ex+e-x,所以F(x1)F(x2)= ≥
≥
 ≥
≥  ,
,
所以F(1)F( n)>en+1+2,F(2)F(n-1)>en+1+2……F(n)F(1)>en+1+2.
由此得,[F(1)F(2)…F(n)]2=[F(1)F(n)][F(2)F(n-1)]…[F(n)F(1)]>(en+1+2)n
故F(1)F(2)…F(n)>(en+1+2) ,n∈N*
…….12分
,n∈N*
…….12分


![]() 中,底面
中,底面![]() 四边长为1的
四边长为1的![]() ,
, ![]() ,
, ![]() ,
,![]() 为
为![]() 的中点.
的中点.![]() ;
;
![]() ,M为AB中点,N为SC中点.
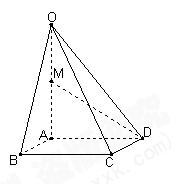
,M为AB中点,N为SC中点.![]() 中,底面
中,底面![]() 是正方形,侧面
是正方形,侧面![]() 是正三角形,平面
是正三角形,平面![]() 底面
底面![]() .证明:
.证明:![]() 平面
平面![]() ;
;