查看答案和解析>>

已知f是直角坐标平面xOy到自身的一个映射，点P在映射f下的象为点Q，记作Q=f(P)，设P₁（x₁，y₁），P₂=f(P₁)，P₃=f(P₂)，…，P_n=f(P_n-1)，…。如果存在一个圆，使所有的点P_n(x_n，y_n)(n∈N*)都在这个圆内或圆上，那么称这个圆为点P_n(x_n，y_n)的一个收敛圆。特别地，当P₁=f(P₁)时，则称点P₁为映射f下的不动点，
(Ⅰ)若点P(x，y)在映射f下的象为点Q(2x，1-y)，
①求映射f下不动点的坐标；
②若P₁的坐标为(1，2)，判断点P_n(x_n，y_n)(n∈N*)是否存在一个半径为3的收敛圆，并说明理由；
(Ⅱ)若点P(x，y)在映射f下的象为点，P₁(2，3)，求证：点P_n(x_n，y_n)(n∈N*)存在一个半径为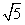的收敛圆。

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

一、选择题

题号

1

2

3

4

5

6

7

8

9

10

11

12

答案

A

A

C

D

C

C

A

C

D

B

B

D

二、填空题

13.3        14.-a、b、-c         15.18             16.(1)(2)

三、解答题

17.解：(1)∵夹角为x,∴cosx=6

S=sin∠ABC=sin(π-x)=sinx                           …………2分

∴                                    …………4分

x∈[0,π],∴x∈[]                                                                              …………6分

(2)f(x)==cos⁴x×1+(-sinx)(sin³x+2sin2x)=cos⁴x-sin⁴x-2sinxcosx

=(cos²x+sin²x)(cos²x-sin²x)-sin²x=cos²x-sin²x=2cos(2x+)                  …………9分

∵

∴f(x)∈[-]                                                                                       …………12分

18.解：(1)从平台达到第一阶每步只能上一阶，因此概率P₁=                …………2分

从平台到达第二阶有二种走法：走两步，或一步到达，

故概率为P₂=×+                                                                      …………5分

(2)该人走了五步，共上的阶数ξ取值为5，6，7，8，9，10

ξ的分布列为：(6分)

ξ

5

6

7

8

9

10

P

()⁵

E_ξ=5×()5+6×    …………12分

19.(1)证：连结A₁D、A₁B

由已知可得△AA₁B和△A₁AD为全等的正三角形.

∴A₁B=A₁D∴A₁O⊥BD

又AB=AD，BD=BD

∴△ABD≌△A₁BD∴A₁O=AO=

又AA₁=2∴A₁O⊥AO

∴A₁O⊥平面ABCD                                                                        …………4分

(2)过C₁作C₁H⊥AC交AC的延长线于H，则C₁H⊥平面ABCD

连结BH，则∠C₁BH为BC₁与平面ABCD所成的角.

∵OH=A₁C₁=2，BO=，∴BH=

∴tan∠C₁BH=∠C₁BH=arctan                       …………8分

((2)也可用向量法求解)

(3)连结OO₁，易知AA₁∥OO₁，面AA₁O₁O⊥面BDD₁B₁

作A₁G⊥OO₁，则A₁G为AA₁与面B₁D₁DB的距离.

由(1)知A₁O=AO=A₁O₁，A₁O⊥A₁O₁

∴A₁G==1                                                                             …………12分

((3)也可用向量法或等积法求解)

20.(1)y²=,∵y²>0,x>0,∴x>3又y<0

  ∴y=-                                                                      …………4分

  (2)x=∴y=f^-1(x)=  (x<0)                                        …………7分

  设(x₀，y₀)为y=f^-1(x)图象上任一点.

  =

  故-                                                                                   …………12分

21.(1)，当n=时，

∴c=                                                                                            …………3分

(2)∵直线x=∴P点在以F为焦点，x=为准线的椭圆上                                                                                …………5分

设P(x,y)则点B(0，-1)代入，解得a=

∴曲线方程为                                                                   …………7分

 (3)设l:y=kx+m(k≠0)与联立，消去y得：(1+3k²)x²+6kmx+3m²-3=0,

  △>0得：m²<3k²+1                                                                         …………9分

  设M(x₁，y₁),N(x₂，y₂),MN中点A(x₀,y₀),由，

  由韦达定理代入K_BA=-，可得到m=

  ∴k²-1<0,∵k≠0,∴-1<k<0或0<k<1                                                 …………11分

  即存在k∈(-1,0)∪(0.1)使l与曲线Q交于两个不同的点M、N

  使                                                                                 …………12分

22.(1)由于数列{a_n}的倒均数，V_n=

得：                                                           …………2分

当n≥2时，所以，又当n=1时，a₁=也适合上式.

∴a_n=                                                                           …………6分

(2)由于{b_n}是公比为q=的等比数列，∴{}为公比为2的等比数列，其倒均数

V_n=，不等式V_n<                                      …………8分

若b₁<0,则2ⁿ-1>8n，令f(x)=2^x-8x-1，则f(x)=2^xln2-8,当x≤3时，f(x)<0,当x>4时，f(x)>0,∴f(x)当x≥4时是增函数又f(x)=-9<0,f(6)=15>0,故当n≥6时，f(n)>0，即2n-1>8n恒成立，因此，存在正整数m，使得当n≥m,n∈N*时，V_n<恒成立，且m的最小值为6……12分

若b₁>0,则上式即为2ⁿ-1<8n,显然当n≤5时成立，而n>5时不成立，故不存在正整数m,使n≥m(n∈N*)时，V_n=成立                                                                 …………14分