
题目列表(包括答案和解析)
如图所示,四面体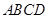 被一平面所截,截面
被一平面所截,截面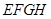 是一个平行四边形.求证:
是一个平行四边形.求证: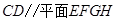 ;
;
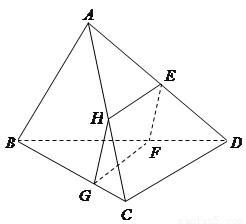
【答案】(理)证明: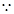 EH∥FG,EH
EH∥FG,EH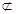 面
面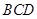 ,
,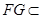 面
面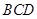
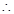 EH∥面
EH∥面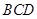 ,又
,又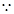 CD
CD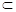 面
面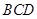 ,
,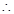 EH∥CD, 又EH
EH∥CD, 又EH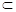 面EFGH,CD
面EFGH,CD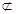 面EFGH
面EFGH
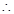 EH∥BD
EH∥BD
【解析】本试题主要是考查了空间四面体中线面位置关系的判定。
要证明线面平行可知通过线线平行,结合判定定理得到结论。
已知正方体ABCD-A1B1C1D1,
O是底面ABCD对角线的交点.
(1)求证:A1C⊥平面AB1D1;
(2)求 .
.

【解析】(1)证明线面垂直,需要证明直线垂直这个平面内的两条相交直线,本题只需证: 即可.
即可.
(2)可以利用向量法,也可以根据平面A1ACC1与平面AB1D1垂直,可知取B1D1的中点E,则 就是直线AC与平面AB1D1所成的角.然后解三角形即可.
就是直线AC与平面AB1D1所成的角.然后解三角形即可.
如图,直线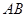 经过⊙
经过⊙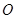 上的点
上的点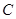 ,并且
,并且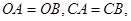 ⊙
⊙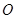 交直线
交直线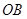 于
于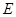 ,
,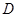 ,连接
,连接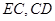 .
.
(I)求证:直线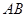 是⊙
是⊙ 的切线;
的切线;
(II)若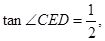 ⊙
⊙ 的半径为
的半径为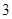 ,求
,求 的长.
的长.
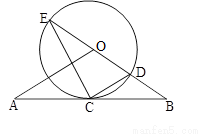
【解析】(1)证明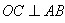 ;(II)根据
;(II)根据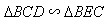 ,
,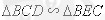
两次相似求得。
设函数 ,若
,若 为函数
为函数 的一个极值点,则下列图象不可能为
的一个极值点,则下列图象不可能为 的图象是
的图象是

【答案】D
【解析】设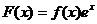 ,∴
,∴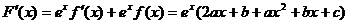 ,
,
又∴ 为
为 的一个极值点,
的一个极值点,
∴ ,即
,即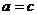 ,
,
∴ ,
,
当 时,
时, ,即对称轴所在直线方程为
,即对称轴所在直线方程为 ;
;
当 时,
时, ,即对称轴所在直线方程应大于1或小于-1.
,即对称轴所在直线方程应大于1或小于-1.
【解析】T,i关系如下图:
| T | 1 |
|
|
|
|
| i | 2 | 3 | 4 | 5 | 6 |
【答案】![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com