练习册

  • 练习册
  • 试题
    加速时由动能定理知:eU0=mv02 -0 ---电子在板中做类平抛L=v0t=at2 a= ∴= 得:U= --------------电子恰从右边沿飞出.由几何关系知: /=(+H)/OPOP=(+H)? -------------② 对整个过程应用动能定理:e (U0+) =mv2-0 得: v= = = ---------- 【查看更多】

     

    题目列表(包括答案和解析)

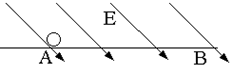    精英家教网如图所示，带负电小球质量为m=1×10-2kg，带电量大小为q=l×10-6C，置于光滑绝缘水平面上且空间存在着斜向下的匀强电场的A点处时，该小球从初速度VA=1.5m/s开始始终沿水平面做匀减速直线运动，当运动到B点时，恰好停止，然后开始反向运动．已知AB之间的距离为S=0.15m，求此匀强电场场强E的取值范围．（ g=10m/s2 ）某同学求解如下：
    设电场方向与水平面之间夹角为θ，由动能定理qEScosθ=0-
    1
    2
    m
    v
    2
    A

    得E=
    -m
    v
    2
    A
    2qScosθ
    =
    75000
    cosθ
    V/m．
    由题意可知θ＞0，所以当E＞7.5×104V/m时小球将始终沿水平面做匀加速直线运动．
    经检查，计算无误．该同学所得结论是否有不完善之处？若有请予以补充．

    查看答案和解析>>

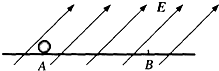    精英家教网如图所示，带正电小球质量为m=1×10-2kg，带电量为q=l×10-6C，置于光滑绝缘水平面上的A点．当空间存在着斜向上的匀强电场时，该小球从静止开始始终沿水平面做匀加速直线运动，当运动到B点时，测得其速度vB=1.5m/s，此时小球的位移为S=0.15m．求此匀强电场场强E的取值范围．（g=10m/s．） 
    某同学求解如下：设电场方向与水平面之间夹角为θ，由动能定理qEScosθ=
    1
    2
    m
    v
    2
    B
    -0得E=
    m
    v
    2
    B
    2qScosθ
    =
    75000
    cosθ
    V/m．由题意可知θ＞0，所以当E＞7.5×104V/m时小球将始终沿水平面做匀加速直线运动．经检查，计算无误．该同学所得结论是否有不完善之处？若有请予以补充．

    查看答案和解析>>

    下面有两种观点是关于粒子从回旋加速器中射出时最大速度vm的大小由哪些因素决定的讨论，你认为正确的是哪种？

    观点一：使粒子获得动能的是电场，设共加速n次，则由动能定理有：

        nqU=m2vm=

        于是得出为了使粒子射出的速度vm最大，只需增大加速电压，而与磁感应强度的大小及D形盒半径大小无关.

    观点二：只要粒子从D形盒中边缘导出，那么，它最后半周应满足

        qvmB=

        要使粒子射出时的速度vm最大，就要使磁场的磁感应强度B及D形盒的半径R大，而与加速电压U的大小无关(只要U≠0).

    查看答案和解析>>

    如图19所示，带正电小球质量为m=1×10-2 kg、带电荷量为q=1×10-6 C,置于光滑绝缘水平面上的A点.当空间存在着斜向上的匀强电场时，该小球从静止开始始终沿水平面做匀加速直线运动，当运动到B点时，测得其速度vb=1.5 m/s,此时小球的位移为s=0.15 m.求此匀强电场场强E的取值范围.（g取10 m/s2）

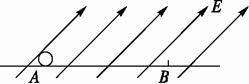
    图19

    某同学求解如下：设电场方向与水平面之间夹角为θ,由动能定理qEscosθ=mvb2-0得由题可知θ＞0，所以当E＞7.5×104 V/m时小球将始终沿水平面做匀加速直线运动.

    经检查，计算无误.该同学所得结论是否有不完善之处？若有，请予以补充.

    查看答案和解析>>

    如图所示，带正电小球质量为m=1×10-2 kg，带电荷量为q=1×10-6 C,置于光滑绝缘水平面上的A点.当空间存在着斜向上的匀强电场时，该小球从静止开始始终沿水平面做匀加速直线运动，当运动到B点时，测得其速度vb=1.5 m/s，此时小球的位移为s=0.15 m.求此匀强电场场强E的取值范围.（g取10 m/s2）

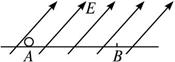
    某同学求解如下：设电场方向与水平面之间夹角为θ,由动能定理qEscosθ=mvB2-0,得E== V/m，由题意可知θ＞0,所以当E＞7.5×104 V/m时小球将始终沿水平面做匀加速直线运动.

    经检查，计算无误.该同学所得结论是否有不完善之处？若有请予以补充.

    查看答案和解析>>


    同步练习册答案