
题目列表(包括答案和解析)
已知![]() 为奇函数,则
为奇函数,则![]() 的一个取值 ( )
的一个取值 ( )
A.0 B.π C.![]() D.
D.![]()
(本题15分)已知函数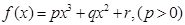 图象的对称中心为
图象的对称中心为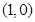 ,且
,且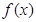 的极小值为
的极小值为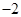 .
.
(1)求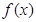 的解析式;
的解析式;
(2)设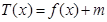 ,若
,若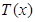 有三个零点,求实数
有三个零点,求实数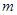 的取值范围;
的取值范围;
(3)是否存在实数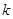 ,当
,当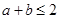 时,使函数
时,使函数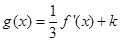
在定义域[a,b] 上的值域恰为[a,b],若存在,求出k的范围;若不存在,说明理由.
(08年黄冈市模拟文) (12分) 已知![]() 记函数
记函数![]() 且
且![]() 最小正周期为2
最小正周期为2![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)判断![]() 在[0,π]上的单调性;
在[0,π]上的单调性;
(3)若![]() 的所有根依次组成一个公差为π的等差数列,求m的值.
的所有根依次组成一个公差为π的等差数列,求m的值.
设 ,
,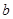 ,
,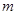 为整数(
为整数( ),若
),若 和
和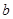 被
被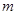 除得的余数相同,则称
除得的余数相同,则称 和
和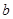 对模
对模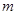 同余,记作
同余,记作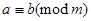 ,已知
,已知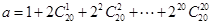 ,且
,且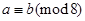 ,则
,则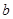 的值可为( ).
的值可为( ).
A.2011 B.2012 C.2009 D.2010
已知函数![]() 图象的对称中心为(0,1);函数
图象的对称中心为(0,1);函数![]() 在 区间[-2,1)上单调递减,在[1, +∞)上单调递增.
在 区间[-2,1)上单调递减,在[1, +∞)上单调递增.
(Ⅰ)求实数b的值;
(Ⅱ)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(Ⅲ)设![]() ,试证:对任意的x1、x2∈(1,+∞)且x1≠x2,都有
,试证:对任意的x1、x2∈(1,+∞)且x1≠x2,都有
![]() .
.
一、选择题
CBCDC BBDDD
二、填空题
11、-6 12、 13、5 14、[1,3
] (2分) [2,5] 15、4
13、5 14、[1,3
] (2分) [2,5] 15、4
16、⑴



三、解答题
17、⑴甲从选择题中抽到一题的可能结果有 个,乙从判断题中抽到一题的可能结果有
个,乙从判断题中抽到一题的可能结果有 个,故甲抽到选择题,乙抽到判断题的可能结果有
个,故甲抽到选择题,乙抽到判断题的可能结果有
 个,又甲、乙依次抽一题的可能结果有
个,又甲、乙依次抽一题的可能结果有 个,所以甲抽到选择题、乙抽到判断题的概率为:
个,所以甲抽到选择题、乙抽到判断题的概率为: (6分)
(6分)
⑵甲、乙二人依次都抽到判断题的概率为 ,故甲、乙二人中至少有一个抽到选择题的概率为
,故甲、乙二人中至少有一个抽到选择题的概率为
或用以下解法:
|