如图，点E在正方形ABCD的边CD上运动，AC与BE交于点F．
（1）如图1，当点E运动到DC的中点时，求△ABF与四边形ADEF的面积之比；
（2）如图2，当点E运动到CE：ED=2：1时，求△ABF与四边形ADEF的面积之比；
（3）当点E运动到CE：ED=3：1时，写出△ABF与四边形ADEF的面积之比；当点E运动到CE：ED=n：1（n是正整数）时，猜想△ABF与四边形ADEF的面积之比（只写结果，不要求写出计算过程）；
（4）请你利用上述图形，提出一个类似的问题

查看答案和解析>>

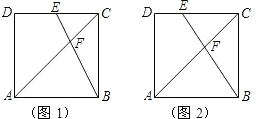
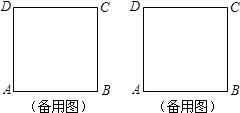
10、如图，点O是正方形ABCD内一点，且OA=OD=AB，则∠OBC的度数为（　　）

A、15°

B、20°

C、25°

D、75°

查看答案和解析>>

16、如图，点A，B，C在同一直线上，且BC=2AB，点D，E分别是AB，BC的中点，分别以AB，DE，BC为边，在A，C同侧作三个正方形，得到三个平行四边形（阴影部分）的面积分别记作S₁，S₂，S₃，若S₁+S₃=5，则S₂=

2

．

查看答案和解析>>

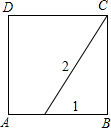如图，点E在正方形ABCD的边AB上，若EB的长为1，EC的长为2，那么正方形ABCD的面积是（　　）

A、 3

B、 5

C、3

D、5

查看答案和解析>>

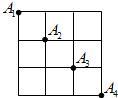29、如图，点A₁，A₂，A₃，A₄是某市正方形道路网的部分交汇点，且它们都位于同一对角线上．某人从点A₁出发，规定向右或向下行走，那么到达点A₃的走法共有（　　）

A、4种

B、6种

C、8种

D、10种

查看答案和解析>>

一、选择题

题号

1

2

3

4

5

6

7

8

9

10

答案

B

D

B

B

C

C

C

B

A

B

二、选择题

11．；12．145；13．20^o；14．大于4万件 15. 内切；16．0.45；17．①②④；18．（-8，0）.

三、解答题

19．解：原式_， 当x＝?0.5时，原式=0.5.

20．解：在Rt△AMN中，AN =MN×tan∠AMN=30×=.在Rt△BMN中,BN =MN×tan∠BMN=30×=.AB=AN-BN=. 则到的平均速度为：AB÷2=÷2=≈17（米/秒）．70千米/时=175÷9米/秒米/秒米/秒，此车没有超过限速．

21．（1）被调查的学生数为（人）.

（2）“教师”所在扇形的圆心角的度数为

（1-15%-20%-10%-×100%）×360°=72°.

（3）补全图如图1，图2，所示.

22．解：（1）如图：， （2） (b，a) 　

（3）由（2）得，D(1,-3) 关于直线l的对称点的

坐标为(-3,1)，连接E交直线l于点Q，此时点Q

到D、E两点的距离之和最小。设过(-3,1)、E(-1,-4)

的直线的解析式为，则

　   ∴   ∴．

由 得  

23．解：（1）过C点作CG⊥AB于G，在Rt△AGC中，

∵sin60°=，∴∵AB=2，

∴S_梯形CDBF=S_△ABC= .

（2）菱形 ∵CD∥BF，FC∥BD，∴四边形CDBF是平行四边形.

∵DF∥AC，∠ACB=90°，∴CB⊥DF   ∴四边形CDBF是菱形.

（3）过D点作DH⊥AE于H，则S_△ADE= 又S_△ADE

=， ∴在Rt△DHE中，sinα=.

24．解：（1）在直角三角尺中，总有∠GDH=90°，

易得∠GDC=∠HDF，又∵ DC=DF∴△GDC≌△HDF

∴GC=HF, 又∵BC=EF∴ BG=EH;

（2）同理可证△DFH≌△DCG ∴  CG=FH,

又∵BC+CG=EF+FH, ∴BG=EH.

25．解:①由题意得与之间的函数关系式（，且x是整数）

②由题意得与之间的函数关系式

③由题意得

∴当x=100时，W_最大=30000，∵100天<160天.∴存放100天后出售这批鸭梨可获得最大利润30000元．

26．解：（1）∵AB∥OC,∴∠OAB=∠AOC=90°,在Rt△OAB中，AB=2,AO=，∴OB=4，

∠ABO=60°，∴∠BOC=60°，而∠BCO=60°，∴△BOC为等边三角形.∴OH=OB?cos30°=.

（2）∵OP=OH-PH= ，过P作y轴的垂线段PG，PG=3- ∴

（），即∴当时，_.

（3）①若为等腰三角形，则：

（i）若,∴∥

∴ 即  解得：

此时.

（ii）若,∠OPM=∠OMP=75°,∴∠OQP ₌=45°.

过点作，垂足为，则有：

即，解得：.

此时.

（iii）若，

∴∥，此时在上，不满足题意.

 ②线段长的最大值为.

本资料由《七彩教育网》www.7caiedu.cn 提供！