
题目列表(包括答案和解析)
(本小题满分12分)
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试
合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是![]() ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(Ⅰ)至少有1人面试合格的概率;
(Ⅱ)签约人数![]() 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分) 甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,
甲先从 道备选题中一次性抽取
道备选题中一次性抽取 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余 题,每人答对其中
题,每人答对其中
题就停止答题,即闯关成功.已知在 道备选题中,甲能答对其中的
道备选题中,甲能答对其中的 道题,乙答对每道题
道题,乙答对每道题
的概率都是 .
.
(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设甲答对题目的个数为ξ,求ξ的分布列及数学期望.
(本小题满分12分)
甲、乙二名射击运动员参加今年深圳举行的第二十六届世界大学生夏季运动会的预选赛,他们分别射击了4次,成绩如下表(单位:环):
| 甲 | 5 | 6 | 9 | 10 |
| 乙 | 6 | 7 | 8 | 9 |
(本小题满分12分)甲、乙等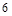 名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为
名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为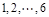 ).
).
(Ⅰ)求甲、乙两考生的面试序号至少有一个为奇数的概率;
(Ⅱ)记在甲、乙两考生之间参加面试的考生人数为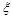 ,求随机变量
,求随机变量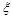 的分布列与期望.
的分布列与期望.
(本小题满分12分)甲、乙等五名环保志愿者被随机地分到 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加 岗位服务的概率;
岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,求
岗位服务的人数,求 的分布列.
的分布列.
一、选择题:1~12(5×12=60)
题号
01
02
03
04
05
06
07
08
09
10
11
12
答案
B
B
A
B
C
D
B
C
B
C
C
D
二、填空题:13、B.files\image047.gif) ;14、-
;14、-.files\image049.gif) ;15、32005;16、(2
;15、32005;16、(2.files\image047.gif) -2,2)。
-2,2)。
三、解答题:
17.解:(1)根据已知条件得:△=16sin2θ-4atanθ=0
即:a=.files\image052.gif) 2sin2θ 2分
2sin2θ 2分
又由已知:.files\image054.gif)
得.files\image056.gif) 4分
4分
所以有0<sin2θ<1
所以a∈(0,2) 6分
(2)当a=.files\image058.gif) 时由(1)得2sin2θ=
时由(1)得2sin2θ=.files\image058.gif) 8分
8分
所以sinθ=.files\image060.gif) ,而sin2θ=-cos(
,而sin2θ=-cos(.files\image062.gif) +2θ)
+2θ)
=-2cos2(.files\image064.gif) )+1=
)+1=.files\image060.gif) 10分
10分
所以cos2(.files\image064.gif) )=
)=.files\image067.gif) ,又
,又.files\image069.gif)
所以cos(.files\image064.gif) )=-
)=-.files\image071.gif) 12分
12分
18.(九A解法)解:(1)取AC、CC1中点分别为M、N,连接MN、NB1、MB1,
∵AC1∥MN,NB1∥CE
∴∠MNB1是CE与AC1成角的补角 2分
Rt△NB.files\image073.gif)
Rt△MNC中,MN=6.files\image075.gif)
Rt△MBB1中,MB1=.files\image077.gif)
∴cos∠MNB1=-.files\image079.gif)
∴CE与AC1的夹角为arccos.files\image079.gif) 4分
4分
(2)过D作DP∥AC交BC于P,则A1D在面BCC1B1上的射影为C1P,而CE⊥A1D,由三垂线定理的逆定理可得CE⊥C1P,又BCC1B为正方形
∴P为BC中点,D为AB中点, 6分
∴CD⊥AB,CD⊥AA1
∴CD⊥面ABB
(3)由(2)CD⊥面A1DE
∴过D作DF⊥A1E于F,连接CF
由三垂线定理可知CF⊥A1E
∴∠CFD为二面角C-A1E-D的平面角 10分
又∵A1D=.files\image082.gif)
∴A1D2+DE2=A1E2=324
∴∠A1DE=90°
∴DF=6.files\image075.gif) ,又CD=6
,又CD=6.files\image075.gif)
∴tan∠CFD=1
∴∠CFD=45°
∴二面角C-A1E-D的大小为45° 12分
(此题也可通过建立空间直角坐标系,运用向量的方法求解)
19.解:由已知得:
不等式x2+px-4x-p+3>0,在p∈[0,4]上恒成立
即:p(x-1)+x2-4x+3>0,在p∈[0,4]上恒成立
令f(p)=p(x-1)+x2-4x+3
则有函数f(p)在p∈[0,4]上大于零恒成立。 4分
(1)显然当x=1时不恒成立
(2)当x≠1时,有.files\image086.gif) 即x>3或x<-1 10分
即x>3或x<-1 10分
所以x∈(3+∞)U(-∞,-1)为所求 12分
20.解:(1)ξ=0、1、2、3
P(ξ=0)=.files\image088.gif)
P(ξ=1)=.files\image090.gif)
P(ξ=2)=.files\image092.gif)
P(ξ=3)= .files\image094.gif)
∴Eξ=1×.files\image096.gif) 6分
6分
(2)设甲考试合格为事件A,乙考试合格为事件B,A、B为相互独立事件
P(A)=P(ξ=2)+P(ξ=3)=.files\image098.gif)
P(B)=.files\image100.gif)
甲、乙两人均不合格为事件.files\image102.gif)
p(.files\image102.gif) )=[1-P(A)][1-P(B)]=
)=[1-P(A)][1-P(B)]=.files\image104.gif)
∴甲、乙两人至少有一人合各的概率为.files\image106.gif) 12分
12分
21.解:(1)∵AB方程是y=3x+1,则.files\image108.gif)
得(1+
∴x A =-.files\image110.gif) ,同理BC方程是y=-
,同理BC方程是y=-.files\image112.gif)
可得xc=.files\image114.gif) 2分
2分
∴|AB|=|xA-0|?.files\image116.gif)
|BC|=|xc-0|?.files\image118.gif) 4分
4分
∵|AB|=|BC|
∴.files\image110.gif)
.files\image120.gif) =
=.files\image114.gif)
.files\image120.gif) 解得a2=
解得a2=.files\image123.gif)
∴椭圆方程为.files\image125.gif) 6分
6分
(2)设AB:y=kx+1(不妨设k>0且k≠1)代入.files\image127.gif)
整理得(1+a2k2)x2+a2kx=0
∴xA=-.files\image129.gif) ,同理xc=
,同理xc=.files\image131.gif) 8分
8分
∴|AB|=.files\image133.gif) ,
,
|BC|=.files\image135.gif)
又|AB|=|BC|
∴.files\image137.gif) 整理得
整理得
(k-1)[k2+(1-a2)k+1]=0 (k≠1)
∴k2+(1-a2)k+1=0 10分
∴△=(1-a2)2-4≥0,解得a≥.files\image047.gif)
若△=0,则a=.files\image047.gif) ,此时k2+[1-(
,此时k2+[1-(.files\image047.gif) )2]k+1=0
)2]k+1=0
.files\image141.gif) k1=k2=1与k≠1矛盾,故a>
k1=k2=1与k≠1矛盾,故a>.files\image047.gif) . 12分
. 12分
22.解:(1)由已知有f′(x)=2n.files\image143.gif)
.files\image145.gif)
令f′(x)=0
得x=±.files\image147.gif) 2分
2分
∵x∈[0,+∞],∴x=.files\image147.gif)
∵0<x<.files\image147.gif) 时f′(x)<0
时f′(x)<0
X>.files\image147.gif) 时f′(x)>0
时f′(x)>0
∴当x=.files\image147.gif) 时,fmin(x)=an=2n
时,fmin(x)=an=2n.files\image150.gif)
=.files\image152.gif) 5分
5分
(2)由已知Tn=cos.files\image154.gif)
=.files\image156.gif) 7分
7分
∵.files\image158.gif) 9分
9分
∴π>.files\image160.gif)
又y=cosx在(0,π)上是减函数
∴Tn是递增的
∴Tn<Tn+1(n∈N*) 10分
(3)不存在
由已知点列An(2n,.files\image152.gif) ),显然满足y2=x2-1,(x=2n) 12分
),显然满足y2=x2-1,(x=2n) 12分
即An上的点在双曲线x2-y2=1上,且在第一象限内
∴任意三点An、Am、Ap连线的斜率KAnAm,KAnAp,KAmAp均为正值。
∴任意两个量的乘积不可能等于-1
∴三角形AnAmAp三个内角均无直角
∴不可能组成直角三角形。 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com