
题目列表(包括答案和解析)
 .
.
(11·肇庆)(本小题满分10分)己知:如图10.△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC干点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA
(2)求证:P处线段AF的中点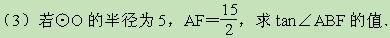 .
.
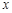 吨, 则粗加工的吨数为 吨,加工这批海产品需要 天, 可获利 元(用含
吨, 则粗加工的吨数为 吨,加工这批海产品需要 天, 可获利 元(用含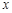 的代数式表示);
的代数式表示);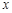 在什么范围内时, 该企业加工这批海产品的获利不低于120000元?
在什么范围内时, 该企业加工这批海产品的获利不低于120000元?
(本小题满分12分)
如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90º.
解答下列问题:
①当点D在线段BC上时(与点B不重合),如图甲,线段CF、BD之间的位置关系为 ,数量关系为 .
②当点D在线段BC的延长线上时,如图乙,①中的结论是否仍然成立,为什么?(要求写出证明过程)
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.且∠BCA=45°时,如图丙请你判断线段CF、BD之间的位置关系,并说明理由(要求写出证明过程).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com