
题目列表(包括答案和解析)
| 1 | 2 |
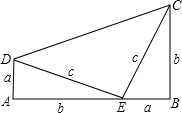
我们知道,一元二次方程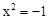 没有实数根,即不存在一个实数的平方等于
没有实数根,即不存在一个实数的平方等于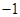 .若我们规定一个新数“
.若我们规定一个新数“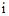 ”,使其满足
”,使其满足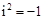 (即方程
(即方程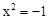 有一个根为
有一个根为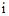 ).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有
).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有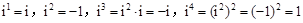 ,从而对于任意正整数
,从而对于任意正整数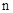 ,我们可以得到
,我们可以得到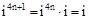 ,同理可得
,同理可得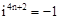 ,
,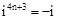 ,
,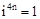 .那么
.那么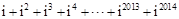 的值为 .
的值为 .
 ab
ab
我们知道,方程![]() 没有实数根,即不存在一个实数的平方等于
没有实数根,即不存在一个实数的平方等于![]() .若我们规定
.若我们规定
一个新数“![]() ”,使其满足
”,使其满足![]() (即方程
(即方程![]() 有一个根为
有一个根为![]() )。并且进一步规定:
)。并且进一步规定:
一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有![]() 1=
1=![]() ,
,
![]() =-1,
=-1,![]() =
= ![]()
![]() =(-1)
=(-1)![]() =-
=-![]() ,
, ![]() =(
=(![]() )2=(-1)2=1从而对于任意正整数
)2=(-1)2=1从而对于任意正整数![]() ,我们可以
,我们可以
得到![]() , 同理可得
, 同理可得![]() ,
, ![]() ,
, ![]() .
.
那么![]() 的值为 ( )
的值为 ( )
A. 0 B. ![]() C.
C.![]() D.
D. ![]()
| 2 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com