
题目列表(包括答案和解析)
(本题满分12分)本题共有2个小题,第1小题满分4分,第2小题满分8分.
已知 ,函数
,函数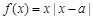 .
.
(Ⅰ)当 时,求使
时,求使 成立的
成立的 的集合;
的集合;
(Ⅱ)求函数 在区间
在区间 上的最小值.
上的最小值.
(本题满分12分)本题共有2个小题,第1小题满分8分,第2小题满分4分.
在正四棱柱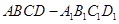 中,已知底面
中,已知底面 的边长为2,点P是
的边长为2,点P是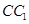 的中点,直线AP与平面
的中点,直线AP与平面 成
成 角.
角.
(文)(1)求 的长;
的长;
(2)求异面直线 和AP所成角的大小.(结果用
和AP所成角的大小.(结果用
反三角函数值表示);
(理)(1)求异面直线 和AP所成角的大小.(结果用
和AP所成角的大小.(结果用
反三角函数值表示) ;
(2)求点 到平面
到平面 的距离.
的距离.

(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分.
如图,已知 平面
平面 ,
, ,
, ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)求异面直线 与
与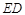 所成的角的大小;
所成的角的大小;
(2)求 绕直线
绕直线 旋转一周所构成的旋转体的体积.
旋转一周所构成的旋转体的体积.
(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分.
已知复数 ,
, (
( ,
, 是虚数单位)。
是虚数单位)。
(1)若复数 在复平面上对应点落在第一象限,求实数
在复平面上对应点落在第一象限,求实数 的取值范围
的取值范围
(2)若虚数 是实系数一元二次方程
是实系数一元二次方程 的根,求实数
的根,求实数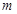 的值.
的值.
(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
如图,在直三棱柱 中,
中,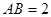 ,
, ,
, .
.
(1)求三棱柱 的表面积
的表面积 ;
;
(2)求异面直线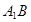 与
与 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).

一、填空题:中国数学论坛网
http://www.mathbbs.cn
1.2 2.4 3.3 4..files/image101.gif) 5.12 6.―2 7.
5.12 6.―2 7..files/image103.gif) 8.
8..files/image105.gif) 9.18
9.18
|