查看答案和解析>>

（本小题满分12分）
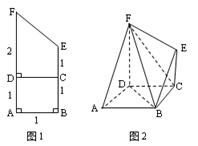
将如图1的直角梯形ABEF（图中数字表示对应线段的长度）沿直线CD折成直二面角，连结EB、FB、FA后围成一个空间几何体如图2所示，
（1）求异面直线BD与EF所成角的大小；
（2）求二面角D—BF—E的大小；
（3）求这个几何体的体积.

查看答案和解析>>

一、选择题

1―5 CCBAD    6―10 BBDBC    11―12 BD

二、填空题

13．0   14．（1）81  （2）1004    15．②③    16．达到标准①未达到标准②

三、解答题：

17．解:（Ⅰ）共有个基本事件，

，，，，，，,，，，，，，,，，，，，,，，，，,，，，,，，,，,，                                      ………………6分

 （Ⅱ）

，,，，,，，，,，，,，,           

.     ………………12分

18．解：设

………………3分

   （2）由题意作BH⊥CG，连结AC

由三视图可知BC⊥平面ABG，∴BC⊥AG

又∵BH⊥平面ACG，∴BH⊥AG

∵AG⊥平面BCG，又∵AGC平面ADG

∴平面BCG⊥平面ADG   …………4分

   （3）由（2）可得AG⊥BG，又∵AG=BG，AB=2a，作GP⊥AB于P

∴平面ABCD⊥平面BAG，∴GP⊥平面ABCD  得GP=a。

20．（1）当n=1时，

   ………………4分

   （2）……

   （3）

求 …………4分

21．（1）当

   （2）

22．（1）三个函数最小值依次为1，

   （2）①

   ………………5分

②