
题目列表(包括答案和解析)
| x-1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| b |
| a-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
| 5π |
| 12 |
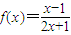 的对称中心是
的对称中心是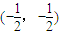 ;
;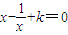 在x∈(0,1)没有实数根,则k的取值范围是k≥2;
在x∈(0,1)没有实数根,则k的取值范围是k≥2;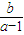 的取值范围为
的取值范围为 ;
;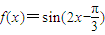 的图象向右平移ϕ(ϕ>0)个单位后变为偶函数,则ϕ的最小值是
的图象向右平移ϕ(ϕ>0)个单位后变为偶函数,则ϕ的最小值是 ;
;| x-1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| b |
| a-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
| 5π |
| 12 |
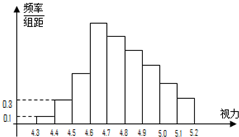 为了解某校高二学生的视力情况,随机地抽查了该校100名高二学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为B,视力在4.6到5.0之间的学生数为F.
为了解某校高二学生的视力情况,随机地抽查了该校100名高二学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为B,视力在4.6到5.0之间的学生数为F.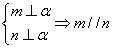 ;(2)
;(2) ;(3)
;(3)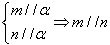 ;
;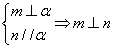 ;(5)α⊥γ,β⊥γ
;(5)α⊥γ,β⊥γ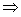 α∥β;
α∥β;
一、选择题(本大题共8小题,每小题5分,满分40分.)
题号
1
2
3
4
5
6
7
8
选项
C
A
C
B
D
B
B
A
二、填空题(共7小题,计30分。其中第9、10、11、12小题必做;第13、14、15题选做两题,若3题全做,按前两题得分计算。)
9、 4 10、__10__(用数字作答).11、____。12、___0___。
13、 ;14、___8_____.15、 3 。
三、解答题(考生若有不同解法,请酌情给分!)
16.解:(1)…………2分
……………………………………3分
………………………………………………5分
(2)…………………………7分
…………………………………9分
………………………………………10分
故
∴当………………………………12分
17.解:⑴、记甲、乙两人同时参加岗位服务为事件,那么,即甲、乙两人同时参加岗位服务的概率是.……………………4分
⑵、记甲、乙两人同时参加同一岗位服务为事件,
那么,…………………………………………………………6分
所以,甲、乙两人不在同一岗位服务的概率是.………8分
⑶、随机变量可能取的值为1,2.事件“”是指有两人同时参加岗位服务,则
.所以,
的分布列是:…………………………………………………………………… 10分
1
2
∴…………………………………………………………12分
18.
解:设2008年末汽车保有量为a1万辆,以后各年末汽车保有量依次为a2万辆,a3万辆,…,每年新增汽车x万辆。………………………………………………………………1分
a1=30,a2=a1×0.94+x,a3=a2×0.94+x=a1×0.942+x×0.94+x,…
故an=a1×0.94n-1+x(1+0.94+…+0.94n-2)
.………………………………………………6分
(1):当x=3万辆时,an≤30
则每年新增汽车数量控制在3万辆时,汽车保有量能达到要求。……………9分
(2):如果要求汽车保有量不超过60万辆,即an≤60(n=1,2,3,…)
则,
即.
对于任意正整数n,
因此,如果要求汽车保有量不超过60万辆,x≤3.6(万辆).………………13分
答:若每年新增汽车数量控制在3万辆时,汽车保有量能达到要求;每年新增汽车不应超过3.6万辆,则汽车保有量定能达到要求。………………………………………14分
19.解:(1)…………………………………………………………2分
由己知有实数解,∴,故…………………5分
(2)由题意是方程的一个根,设另一根为
则,∴……………………………………………………7分
∴,
当时,;当时,;
当时,
∴当时,有极大值,又,,
即当时,的量大值为 ………………………10分
∵对时,恒成立,∴,
∴或………………………………………………………………13分
故的取值范围是 ………………………………………14分
20.解:(1)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连结PQ,依题意可得MP∥NQ,且MP=NQ,即MNQP是平行四边形,
∴MN=PQ.由已知,CM=BN=a,CB=AB=BE=1,
∴AC=BF=, .
即CP=BQ=.
∴MN=PQ=
(0<a<).…………………………………5分
(2)由(Ⅰ),MN=,所以,当a=时,MN=.
即M、N分别移动到AC、BF的中点时,MN的长最小,最小值为.………8分
(3)取MN的中点G,连结AG、BG,∵AM=AN,BM=BN,G为MN的中点
∴AG⊥MN,BG⊥MN,∠AGB即为二面角α的平面角,………………………11分
又AG=BG=,所以,由余弦定理有cosα=.
故所求二面角的余弦值为-.………………………………………………………14分
(注:本题也可用空间向量,解答过程略)
21.解:⑴、对任意的正数均有且.
又
,…………………………………………………4分
又是定义在上的单增函数,.
当时,,.,.
当时,,
.,
为等差数列,,. ……………………………6分
⑵、假设存在满足条件,即
对一切恒成立.
令,
,………………………10分
故,………………………12分
,单调递增,,.
.……………………………………………………………14分
(考生若有不同解法,请酌情给分!)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com