
题目列表(包括答案和解析)
函数![]() 的图象经过怎样的变换可以得到
的图象经过怎样的变换可以得到![]() 的图象( )
的图象( )
A、向左平移1个单位,再向下平移1个单位 B、向左平移1个单位,再向上平移1个单位
C、向右平移1个单位,再向上平移1个单位 D、向右平移1个单位,再向下平移1个单位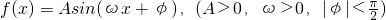 的图象,它与y轴的交点为(
的图象,它与y轴的交点为(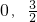 ),它在y轴右侧的第一个最大值点和最小值点分别为(x0,3),(x0+2π,-3).
),它在y轴右侧的第一个最大值点和最小值点分别为(x0,3),(x0+2π,-3).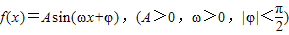 的图象,它与y轴的交点为(
的图象,它与y轴的交点为(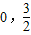 ),它在y轴右侧的第一个最大值点和最小值点分别为(x,3),(x+2π,-3).
),它在y轴右侧的第一个最大值点和最小值点分别为(x,3),(x+2π,-3).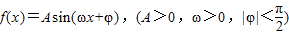 的图象,它与y轴的交点为(
的图象,它与y轴的交点为(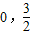 ),它在y轴右侧的第一个最大值点和最小值点分别为(x,3),(x+2π,-3).
),它在y轴右侧的第一个最大值点和最小值点分别为(x,3),(x+2π,-3).| 2π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
福州八中2006级高中数学选修4-2模块考试
一、选择题 BDAC
二、填空题
|