题目列表(包括答案和解析)
（本小题满分12分）甲、乙两人准备参加中央电视台组织的奥运志愿者选拔测试。已知在备选的10道试题中，甲能答对其中的6道，乙能答对其中 的8道。规定每次考试都从备选题中随机抽出3道进行测试，至少答对2道才能入选。
（1）求甲答对试题数
的概率分布及数学期望。
（2）求甲、乙两人至少有一人入选的概率。
（本小题满分12分）
甲、乙两位学生参加数学竞赛培训，现分别从他们的培训期间参加的若干次预赛成中随机抽取8次，记录如下
甲：82，91，79，78，95，88，83，84
乙：92，95，80，75，83，80，90，85
（I） 画出甲、乙两位学生成绩的茎叶图；
（II） 现要从中选派一人参加数学竞赛，从统计学角度，你认为派哪位学生参加合请说明理由。
（III）
若将频率视为概率，对学生甲在今后的三次数学竞赛成绩进行预测，记这三次成绩中高于80分的次数为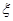
，求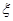的分布列及数学期望E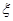
（本小题满分12分）
甲、乙两位学生参加数学建模竞赛培训，现分别从他们在培训期间参加的若干次预
赛成绩中随机抽取8次，记录如下：
甲：72 71 69 68 85 78 83 74
乙：82 85 70 65 73 70 80 75
（Ⅰ）画出甲、乙两位学生成绩的茎叶图，指出学生乙成绩的中位数；
（Ⅱ）现要从中选派一人参加数学建模竞赛，从平均状况和方差的角度考虑，你认为派哪位学生参加合适?请说明理由；
（Ⅲ）若将频率视为概率，对学生甲在今后的三次数学建模竞赛成绩进行预测，记这三次成绩中高于80分的次数为ξ，求ξ的分布列及数学期望Eξ．
（本小题满分12分）
甲、乙两位学生参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，记录如下：
甲：82 81 79 78 95 88 93 84
乙：92 95 80 75 83 80 90 85
（1）用茎叶图表示这两组数据，并写出乙组数据的中位数；
（2）经过计算知甲、乙两人预赛的平均成绩分别为
，甲的方差为
，现要从中选派一人参加数学竞赛，你认为选派哪位学生参加较合适？请说明理由；
（3）现规定80分以上为合格成绩，90分以上为优秀成绩，从甲的合格成绩中随机抽出2个，则抽出优秀成绩的概率有多大？
（本小题满分12分）
甲、乙两位学生参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，记录如下：
甲：82 81 79 78 95 88 93 84
乙：92 95 80 75 83 80 90 85
（1）用茎叶图表示这两组数据，并写出乙组数据的中位数；
（2）经过计算知甲、乙两人预赛的平均成绩分别为
，甲的方差为
，现要从中选派一人参加数学竞赛，你认为选派哪位学生参加较合适？请说明理由；
（3）现规定80分以上为合格成绩，90分以上为优秀成绩，从甲的合格成绩中随机抽出2个，则抽出优秀成绩的概率有多大？
一、
1．B 2．A 3．D 4．D 5．C 6．B 7．A 8．C 9．D 10．A
11．A 12．B
1．由题意知
，解得
或
，故选B．
2．原不等式即为
，化得
，解得
．故选A．
3．由条件
．对上
，所以
又
，所以
．故选D．
4．设
到
的角为
的斜率
的斜率
，
则
，于是
．故选D．
5．由
解得
，即其反函数为
，又在原函数中由
得
，即其反函数中
．故选C．
6．不等式组化得 
或
平面区域如图所示，阴影部分面积：
，故选B．
7．由已知得
，而
．故选A．
8．
．故选c．
9．令
，则
，即
的图象关于（0，0）点对称，将的图象向下平移6个单位．得题中函数的图象，则它的对称中心为（0，
）．故选D．
10．
．故选A．
11．由条件得：
，则
得
，所以
．故选A．
12．由已知正三棱柱的高为球的直径，底面正三角形的内切圆是球的大圆．设底面正三角形的边长为
，球半径为
，则
，又
，解得
，则
，于是
．故选B．
二、
13．
与
平行，
，解得
即
14．设数列
的公比为
，则
，两式相除，得
，则
．
所以
．
15．由题意知，直线
是抛物线
的准线，而
到的距离等于到焦点
的距离．即求点到点
的距离与到点
的距离和的最小值，就是点与点的距离，为
．
16．一方面．由条件，
，得
，故②正确．
另一方面，如图，在正方体
中，把
、
分别记作、
，平面
、平面
、平面
分别记作
、
、
，就可以否定①与③．
三、
17．解：
，且
，即
又
．
由正弦定理
又
即
的取值范围是区间
．
18．解：（1）设甲、乙两人通过测试的事件分别为、
，则
，
、相互独立，∴甲、乙两人中只有1人通过测试的概率
．
（2）甲答对题数
的所有可能值为
∴甲答对题数的数学期望为
．
19．解：（1）由已知
，∴数列
的公比
，首项
又数列
中，
的公差
，首项
（
时也成立）
∴数列、
的通项公式依次为
．
（2）记
当
时，
和
都是增函数
即时，
是增函数
当
4时，
；
又
时
或，∴不存在
，使
．
20．（1）证明；在直三棱柱
中，
面
又
面
，而
面
，
∴平面
平面
（2）解：取
中点
，连接
交
于点，则
．
与平面所成角的大小等于与平面所成角的大小，取
中点
，连接
、
，则等腰三角形
中，
．
又由（1）得
面
．
面
为直线与面所成的角
又
，
∴直线与平面所成的角为
．
（注：本题也可以能过建立空间直角坐标系解答）
21．解：（1）设椭圆方程为
，双曲线方程为
，半焦距
由已知得
，解得
，则
故椭圆及双曲线方程分别为
及
．
（2）由向量的数量积公式知，
表示向量
与
夹角的余弦值，设
，即求
的值．
由余弦定理得
①
由椭圆定义得 
②
由双曲线定义得
③
式②+式③得
，式②一式③
得
将它们代人式①得
，解得
，
所以
．
22，解：（1）由
得
要使在（0，1]上恒为单调函数，只需
或
在（0，1]上恒成立．
∴只需
或
在（0，1]上恒成立
记
或
（2）
，
∴由
得
化简得
时有
，即
，
则
①
构造函数
，则
在
处取得极大值，也是最大值．
在
范围内恒成立，而
从而
在范围内恒成立．
∴在
时，
而
时，
，∴当
时，
恒成立
即时，总有
②
由式①和式②可知，实数的取值范围是
．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com