
题目列表(包括答案和解析)
连接椭圆 的一个焦点和一个顶点得到的直线方程为
的一个焦点和一个顶点得到的直线方程为 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )
A. B.
B. C.
C.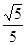 D.
D.
连接椭圆 的一个焦点和一个顶点得到的直线方程为
的一个焦点和一个顶点得到的直线方程为 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )
A. B.
B. C.
C. D.
D.
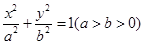 的一个焦点和一个顶点得到的直线方程为
的一个焦点和一个顶点得到的直线方程为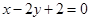 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )A. | B. | C. | D. |
 的一个焦点和一个顶点得到的直线方程为x-2y+2=0,则该椭圆的离心率为
的一个焦点和一个顶点得到的直线方程为x-2y+2=0,则该椭圆的离心率为[ ]




| x2 |
| a2 |
| y2 |
| b2 |
一、选择题:
1―5 ADCBC 6―10 BDCAA
二、填空题:
11.―2 12.20 13.π 14.卷.files/image134.gif) 15.
15.卷.files/image136.gif) 16.
16.卷.files/image138.gif) 17.①④
17.①④
三、解答题:
18.解:(1)卷.files/image140.gif) ………………3分
………………3分
(2)记“一个标号是
所以卷.files/image142.gif) ………………3分
………………3分
(3)随机变量ξ的分布列为
ξ
0
1
2
3
4
P
卷.files/image144.gif)
卷.files/image146.gif)
卷.files/image148.gif)
卷.files/image148.gif)
卷.files/image146.gif)
(3)Eξ=2.4 ………………8分
19.(本题14分)
解:(1)变式得:卷.files/image150.gif) ………………4分
………………4分
原式卷.files/image152.gif) ; …………3分
; …………3分
(2)解1Q∠AOB=β―α,作OD⊥AB于D,
|