
题目列表(包括答案和解析)
| 分组 | 频数 | 百分比 |
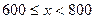 | 2 | 5% |
800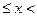 1000 1000 | 6 | 15% |
1000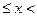 12000 12000 | | 45% |
| | 9 | 22.5% |
| | | |
1600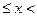 1800 1800 | 2 | |
| 合计 | 40 | 100% |
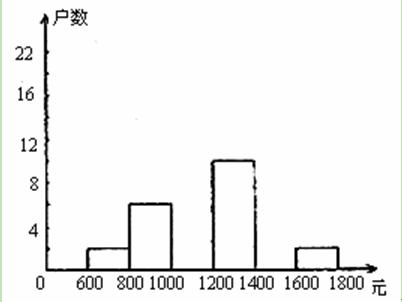
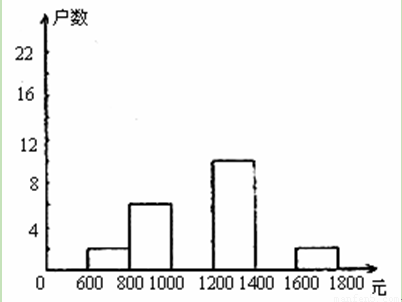
(本小题满分10分)李华在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
| 分组 | 频数 | 百分比 |
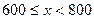 | 2 | 5% |
800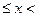 1000 1000 | 6 | 15% |
1000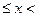 12000 12000 | | 45% |
| | 9 | 22.5% |
| | | |
1600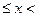 1800 1800 | 2 | |
| 合计 | 40 | 100% |

(本小题满分10分)李华在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
|
分组 |
频数 |
百分比 |
|
|
2 |
5% |
|
800 |
6 |
15% |
|
1000 |
|
45% |
|
|
9 |
22.5% |
|
|
|
|
|
1600 |
2 |
|
|
合计 |
40 |
100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
(本小题满分10分)李华在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
| 分组 | 频数 | 百分比 |
|
| 2 | 5% |
| 800 | 6 | 15% |
| 1000 |
| 45% |
|
| 9 | 22.5% |
|
|
|
|
| 1600 | 2 |
|
| 合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com