练习册

  • 练习册
  • 试题
    (3)对函数＝+和＝+(常数＞0)作出推广.使它们都是你所推广的函数的特例．研究推广后的函数的单调性(只须写出结论.不必证明).并求函数＝+(是正整数)在区间[.2]上的最大值和最小值． 【查看更多】

     

    题目列表(包括答案和解析)

    规律是数学研究的重要内容之一．初中数学中研究的规律主要有一些特定的规则、符号(数)及其运算规律、图形的数值特征和位置关系特征等方面．

    请你解决以下与数的表示和运算相关的问题：

    (1)写出奇数a用整数n表示的式子；

    (2)写出有理数b用整数m和整数n表示的式子；

    (3)函数的研究中，应关注y随x变化而变化的数值规律(课本里研究函数图象的特征实际上也是为了说明函数的数值规律)．

    下面对函数y＝x2的某种数值变化规律进行初步研究：

    xi

    0

    1

    2

    3

    4

    5

    …

    yi

    0

    1

    4

    9

    16

    25

    …

    yi＋1－yi

    1

    3

    5

    7

    9

    11

    …

    由表看出，当x的取值从0开始每增加1个单位时，y的值依次增加1，3，5…

    请回答：

    当x的 取值从0开始每增加个单位时，y的值变化规律是什么？

    当x的取值从0开始每增加个单位时，y的值变化规律是什么？

    查看答案和解析>>

    某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价y1（元）与销售月份x（月）满足关系式y1=-
    14
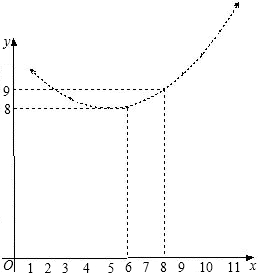    x+20    ，而其每千克成本y2（精英家教网元）与销售月份x（月）满足的函数关系y2=ax2-10ax+c，其图象如图所示．
    （1）求y2的解析式；
    （2）问这种水产品下半年几月份出售每千克的利润最大？最大利润是多少？

    查看答案和解析>>

    某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价y1（元）与销售月份x（月）满足关系式y1=-
    3
    8
    x+36，而其每千克成本y2（元）与销售月份x（月）满足函数关系式
    y2=
    1
    8
    x2-
    15
    8
    x+29
    1
    2
    ．
    （1）求出这种水产品每千克的利润y（元）与销售月份x（月）之间的函数关系式．
    （2）“五一”之前，几月份出售这种水产品每千克的利润最大？最大利润是多少？

    查看答案和解析>>

    画图求方程x2=-x+2的解，你是如何解决的呢？我们来看一看下面两位同学不同的方法．
    甲：先将方程x2=-x+2化为x2+x-2=0，再画出y=x2+x-2的图象，观察它与x轴的交点，得出方程的解；
    乙：分别画出函数y=x2和y=-x+2的图象，观察它们的交点，并把交点的横坐标作为方程的解．
    你对这两种解法有什么看法？请与你的同学交流．

    查看答案和解析>>

    （2012•白下区一模）（1）在学习《二次函数的图象和性质》时，我们从“数”和“形”两个方面对二次函数y=x2和y=（x+3）2进行了研究，现在让我们重温这一过程．
    ①填表（表中阴影部分不需填空）：
    x … -6 -5 -4 -3 -2 -1 0 1 2 3 …
    y=x2 … ▲ ▲ ▲ ▲ ▲ ▲ ▲ …
    y=（x+3）2 … ▲ ▲ ▲ ▲ ▲ ▲ ▲ …
    ②从对应点的位置看，函数y=x2的图象与函数y=（x+3）2的图象的位置有什么关系？
    （2）借鉴（1）中研究的经验，解决问题：
    ①把函数y=2x的图象向
    左
    左
    （填“左”或“右”）平移
    3
    3
    个单位长度可以得到函数y=2x+6的图象．
    ②直接写出函数y=
    k
    x-m
    （k、m是常数，k≠0，m＞0）的两条不同类型的性质．

    查看答案和解析>>


    同步练习册答案