
题目列表(包括答案和解析)
 22、已知函数y=x2-4x+1
22、已知函数y=x2-4x+1阅读材料:若a,b都是非负实数,则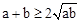 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
证明:∵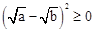 ,∴
,∴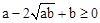 .
.
∴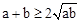 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
举例应用:已知x>0,求函数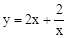 的最小值.
的最小值.
解: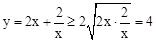 .当且仅当
.当且仅当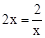 ,即x=1时,“=”成立.
,即x=1时,“=”成立.
当x=1时,函数取得最小值,y最小=4.
问题解决:汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油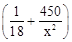 升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
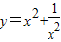 的最小值”提出各自的想法.甲说:“可以用配方法,把它配成
的最小值”提出各自的想法.甲说:“可以用配方法,把它配成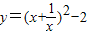 ,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成
,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成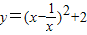 ,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.
,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.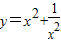 的最小值”提出各自的想法.甲说:“可以用配方法,把它配成
的最小值”提出各自的想法.甲说:“可以用配方法,把它配成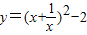 ,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成
,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成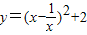 ,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.
,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.如果两个正数 ,即
,即![]() ,有下面的不等式:
,有下面的不等式:
![]() 当且仅当
当且仅当![]() 时取到等号
时取到等号
我们把 叫做正数
叫做正数![]() 的算术平均数,把
的算术平均数,把![]() 叫做正数
叫做正数![]() 的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
例:已知 ,求函数
,求函数![]() 的最小值。
的最小值。
解:令 ,则有
,则有![]() ,得
,得![]() ,当且仅当
,当且仅当![]() 时,即
时,即![]() 时,函数有最小值,最小值为
时,函数有最小值,最小值为![]() 。
。
根据上面回答下列问题
1.已知 ,则当
,则当![]() 时,函数
时,函数![]() 取到最小值,最小值
取到最小值,最小值
为
2.用篱笆围一个面积为![]() 的矩形花园,问这个矩形的长、宽各为多少时,所
的矩形花园,问这个矩形的长、宽各为多少时,所
用的篱笆最短,最短的篱笆周长是多少
3.已知![]() ,则自变量
,则自变量![]() 取何值时,函数
取何值时,函数![]() 取到最大值,最大值为多少?
取到最大值,最大值为多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com