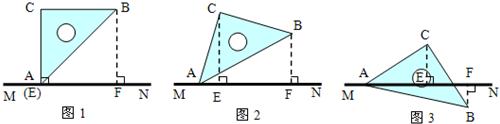
23、平面内两条直线l₁∥l₂，它们之间的距离等于a．一块正方形纸板ABCD的边长也等于a．现将这块硬纸板如图所示放在两条平行线上．
（1）如图1，将点C放置在直线l₂上，且AC⊥l₁于O，使得直线l₁与AB、AD相交于E、F，证明：△AEF的周长等于2a；
请你继续完成下面的探索：
（2）如图2，若绕点C转动正方形硬纸板ABCD，使得直线l₁与AB、AD相交于E、F，试问△AEF的周长等于2a还成立吗？并证明你的结论；
（3）如图3，将正方形硬纸片ABCD任意放置，使得直线l₁与AB、AD相交于E、F，直线l₂与BC、CD相交于G，H，设△AEF的周长为m₁，△CGH的周长为m₂，试问m₁，m₂和a之间存在着什么关系？试证明你的结论．

24、平面内的两条直线有相交和平行两种位置关系

（1）如图a，若AB∥CD，点P在AB、CD外部，则有∠B=∠BOD，又因∠BOD是△POD的外角，故∠BOD=∠BPD+∠D，得∠BPD=∠B-∠D．将点P移到AB、CD内部，如图b，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何数量关系？请证明你的结论；
（2）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？（不需证明）
（3）根据（2）的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．

4、平面上给定了2n个点，其中任意三点不共线，并且n个点染成了红色，n个点染成了蓝色，
证明：总可以找到两两没有公共点的n条直线段，使得其中每条线段的两个端点具有不同的颜色．

23、平面内的两条直线有相交和平行两种位置关系．

（1）AB∥CD．如图a，点P在AB、CD外部时，∠BOD，∠BPD，∠D之间有何数量关系？请说明理由；
（2）如图b，将点P移到AB、CD内部，∠BPD、∠B、∠D之间又有何数量关系？请说明理由；
（3）在图b中，若∠B=40°，∠D=25°，则∠BPD的度数是多少？
（4）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？（不需证明）．

16、平面内有一等腰直角三角板（∠ACB=90°）和一直线MN．过点C作CE⊥MN于点E，过点B作BF⊥MN于点F．当点E与点A重合时（如图1），易证：AF+BF=2CE．当三角板绕点A顺时针旋转至图2、图3的位置时，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段AF、BF、CE之间又有怎样的数量关系，请直接写出你的猜想，不需证明．